Home - Page d'accueil
- Tutoriel POV-Ray
Boucles avec
Sinus, Cosinus
et POV-Ray
>1. Ondes linéaires.
2. Ondes
concentriques.
3. Tapis volants.
- Téléchargement
|
Sinus et cosinus linéaires.
|
Avec cette description je veux démontrer quelques jeux avec les fonctions sinus et cosinus.
L'exemple suivant d'une boucle imbriquée démontre quelches choses élémentaires sur boucles.
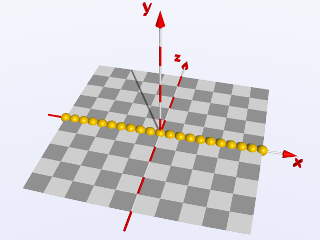
D'abord nous considérons une boucle simple qui place de petites sphères le long de l'axe de x, de
x = 5 à x = +5 :
|
#declare Ball =
sphere{<0,0,0>,0.25
texture{
pigment{color rgb<1,0.8,0>}
finish {diffuse 0.9 phong 1}
}// fin de texture
}// fin de sphere
//----------------------------------
#declare X = -5; // start value X
#declare EndX = 5; // end value X
#declare Step = 0.5;// step value
// début de boucle
#while ( X < EndX + Step)//loop start
object{ Ball translate <X,0,0>}
#declare X = X + Step; // next X
#end // ------ fin de boucle ------- |
|
|
|
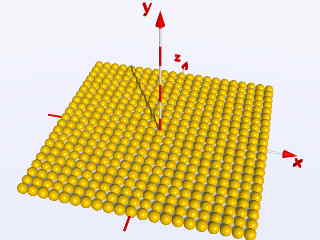
Si nous imbriquons une boucle existante dans une autre boucle, faisant un pas de la valeur z de
z = 0 à z = +5, nous obtenons un carré couvert par des sphères :
|
#declare Z = -5; // start value Z
#declare EndZ = 5; // end value Z
#declare Step = 0.5;// step value
// début de boucle Z:
#while ( Z < EndZ + Step)
#declare X = -5; // start value X
#declare EndX = 5;// end value X
//début de boucle X:
#while ( X < EndX + Step)
object{ Ball translate <X,0,Z>}
#declare X = X + Step;//next X
#end // ------ fin de boucle X
#declare Z = Z + Step; //next Z
#end // ------- fin de boucle Z |
|
|
|
Jusqu'ici l'information sans détours sur boucles while !
Maintenant nous voulons mettre de l'entrain et rythme dans cet région :
Pour faire cela nous avons besoin de le fonctions de sinus ou de cosinus - en POV-Ray
décrit par sin(A) respectivement cos(A)
et ici A est le valeur del'angle en radian.
Si nous utilisons pour la boucle imbriquée précédente :
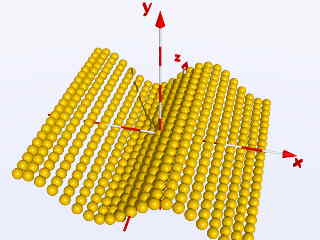
object{ Ball translate < X,
sin(X), Z> }
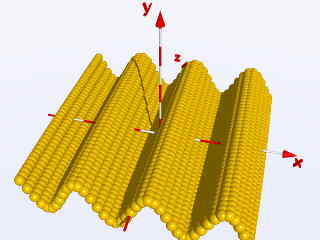
ou avec le pas moitié moins grand : Step = 0.25;
object{ Ball translate < X,
sin(2*X), Z> }
nous obtenons ces images :
|
|