//-----------------------------------------
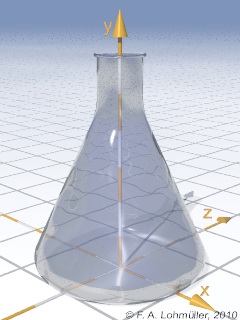
#macro Erlenmeyer_Shape_1 (
Base_H, // base height
Base_Half_Width,// half base radius
Neck_Len, // neck lenght
Neck_R, // neck radius
Fillet_R, // = r1 < Base_H -2*r2
Base_Border_R,//= r2 + r1 < Base_H
Merge_On, //
) //---------------------------------
//-----------------------------------------
#local D = 0.0001 ;
//-----------------------------------------
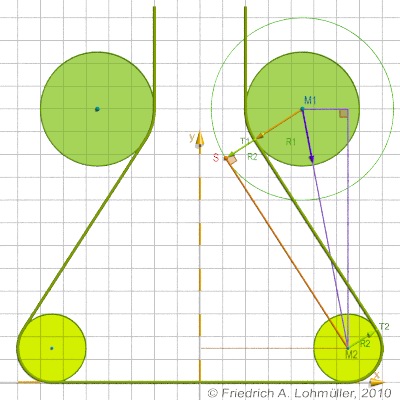
#local R1 = Fillet_R;
#local X1 = (Neck_R+Fillet_R);
#local Y1 = Base_H;
#local M1 = < X1,Y1,0>;
// basis torus cross-section
#local R2 = Base_Border_R;
#local X2 = Base_Half_Width-Base_Border_R;
#local Y2 = Base_Border_R;
#local M2 = <X2,Y2,0>;
//-----------------------------------------
// angle between x-direction and (M1,M2) :
#if (X1 < X2)
#local Cone_Angle =
180-abs(atan((Y2-Y1)/abs(X2-X1)));
#else
#local Cone_Angle =
abs(atan((Y2-Y1)/(X2-X1)));
#end
//-----------------------------------------
// distance M1,M2 via Pythagoras:
#local M_Dist =
sqrt(pow(X2-X1,2)+pow(Y2-Y1,2));
#local M2_S =
sqrt(pow(M_Dist,2)-pow(R1+R2,2));
// Winkel bei M1 in Dreieck S_M1_M2:
#local In_Angle = abs(asin(M2_S/M_Dist)));
#local X_Angle = Cone_Angle-In_Angle ;
#local XSi = X1-(R1+R2)*cos(X_Angle);
#local YSi = Y1-(R1+R2)*sin(X_Angle);
#local Si =<XSi,YSi,0>;
// oberer Tangentenpunkt
#local T1 =
M1-<R1*cos(X_Angle),R1*sin(X_Angle),0>;
// unterer Tangentenpunkt
#local T2 =
M2+<R2*cos(X_Angle),R2*sin(X_Angle),0>;
// the body -------------------------------
#if ( Merge_On = 1 ) merge{
#else union{
#end
// neck
cylinder{<0,-D,0gt;,
<0,Neck_Len,0>,Neck_R
translate<0,M1.y,0> }
// fillet
difference{
cylinder{<0,T1.y-D,0>,
<0,M1.y,0>,T1.x}
torus{ X1,R1 translate<0,Y1,0>}
} // end of difference
// base cone
cone{<0,T2.y,0>,T2.x,
<0,T1.y,0>,T1.x}
// base round + center fill
cylinder{<0,-R2,0>,
<0,R2,0>, X2
translate<0, Y2,0>}
torus{ X2, R2 translate<0, M2.y,>}
} // end of union or merge
#end //----------------------- end of macro
//----------------------------------------- |