Home
- POV-Ray Tutorial
Loops,
Sine, Cosine
and POV-Ray
>1. Linear Waves
2. Concentric waves
3. Flying Carpets
- Download
|
Sine and Cosine linear
|
This description wants to demonstrate some games with sine and cosine function.
Some basics about loops will show the following sample of a double nested while loop.
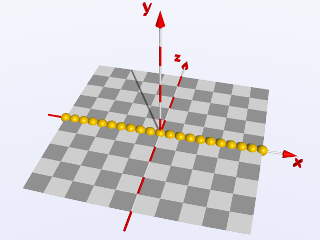
First we consider a simple loop which places little spheres along the x axis between
x = 5 bis x = +5:
|
#declare Ball =
sphere{<0,0,0>,0.25
texture{
pigment{color rgb<1,0.8,0>}
finish {diffuse 0.9 phong 1}
}// end of texture
}// end of sphere
//------------------------------------
#declare X = -5; // start value X
#declare EndX = 5; // end value X
#declare Step = 0.5;// step value
#while ( X < EndX + Step)//loop start
object{ Ball translate <X,0,0>}
#declare X = X + Step; // next X
#end // ------------------- loop end |
|
|
|
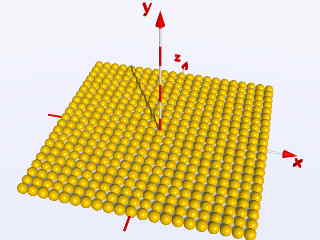
If you nest the existing loop in an additional loop, which runs throug the z-values
between z = -5 bis z = +5, you will get a quadratic area which is
totally covered by spheres:
|
#declare Z = -5; // start value Z
#declare EndZ = 5; // end value Z
#declare Step = 0.5;// step value
// loop start Z:
#while ( Z < EndZ + Step)
#declare X = -5; // start value X
#declare EndX = 5;// end value X
//loop start X:
#while ( X < EndX + Step)
object{ Ball translate <X,0,Z>}
#declare X = X + Step;//next X
#end // ----------- loop end X
#declare Z = Z + Step; //next Z
#end // ------------ loop end Z |
|
|
|
So far the necessary quick information about loops!
Now we want to bring some rythmic movement in this area.
To do this we need to use the sine or the cosine function - in POV-Ray
described by sin(A) respectively cos(A)
and here A is the value of the angle messured in radians.
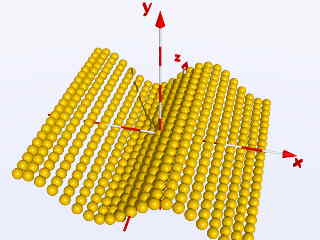
Do we change the previous nested loop in the following way:
object{ Ball translate < X,
sin(X), Z> }
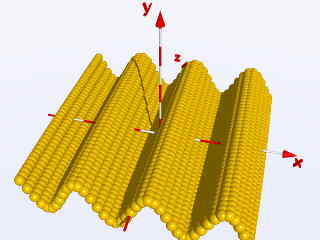
or with the half value for the steps: Step = 0.25
object{ Ball translate < X,
sin(2*X), Z> }
we will get these images:
|
|