Home
- POV-Ray Tutorial
Loops,
seni e coseni
in POV-Ray
>1. Onde lineare
2. Gira e rigira...!
Onde concentriche
3. Tappeti volanti
- Download
|
Seni e coseni in onde lineare
|
Questa descrizione mostra alcuni giochi che possono essere fatti con seni e coseni.
Il seguente esempio illustra anche l'uso di due cicli while nidificati.
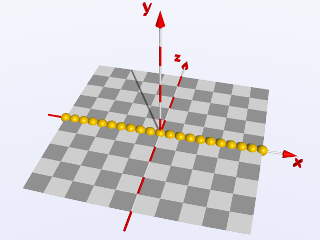
In primo luogo consideriamo un ciclo semplice che posizioni delle piccole sfere lungo
l'asse X tra i punti X = -5 e X = +5:
|
#declare Ball =
sphere{<0,0,0>,0.25
texture{
pigment{color rgb<1,0.7,0>}
finish {ambient 0.1
diffuse 0.9 phong 1}
}// end of texture
}// end of sphere
//------------------------------------
#declare X = -5; // start value X
#declare EndX = 5; // end value X
#declare Step = 0.5;// step value
#while ( X < EndX + Step)//loop start
object{ Ball translate <X,0,0>}
#declare X = X + Step; // next X-Wert
#end // ------------------- loop end |
|
|
|
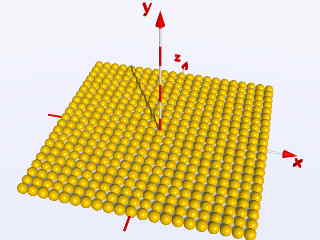
Se aggiungete un secondo ciclo che si sposti lungo l'asse delle Z
tra Z = -5 e Z = +5, avrete un'area quadrata riempita di sfere:
|
#declare Z = -5; // start value Z
#declare EndZ = 5; // end value Z
#declare Step = 0.5;// step value
// loop start Z:
#while ( Z < EndZ + Step)
#declare X = -5; // start value X
#declare EndX = 5; // end value X
//loop start X
#while ( X < EndX + Step)
object{ Ball translate <X,0,Z>}
#declare X = X + Step;//next X-Wert
#end // ---------------- loop end X
#declare Z = Z + Step; //next Z-Wert
#end // ----------------- loop end Z |
|
|
|
Dopo averla creata con queste prime informazioni sui cicli,
dobbiamo dare un po' di movimento a quest'area.
Per farlo dobbiamo utilizzare le funzioni di seno e coseno
definite rispettivamente da sin(A) e cos(A) dove A sia un
angolo misurato in radianti. Modifichiamo dunque il programma come segue:
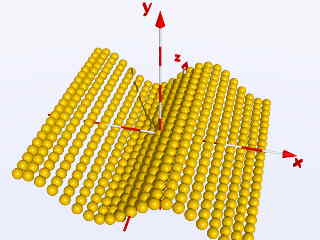
object{ Ball translate < X, sin(X), Z> }
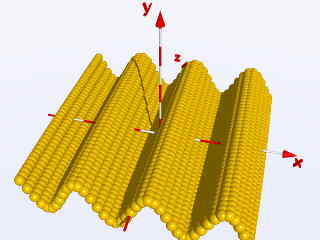
o dimezzando il valore dell'intervallo: Step = 0.25
object{ Ball translate < X, sin(2*X), Z> }
otteniamo queste immagini:
|
|