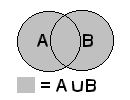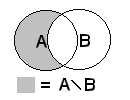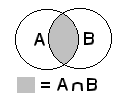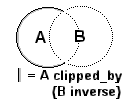Qui una introduzione breve a qualche dei principi fondamentali della costruzione di solidi nuove e più complessi combinando forme primitive. Per questo usiamo la tecnica chiamata 'CSG' (in italiano: Geometria Solida Costruttiva), che usa - descritto brevemente - gli stessi operazioni con solidi come siamo abituato al algebra booleana e anche un po' di più. I questo caso un solido e considerato come un insieme di punti nello spazio tridimensionale. Con questo insieme di punti possiamo lavorare con le operazioni booleane per insiemi.
    Oggetti CSG: Queste operazioni si può usare con tutti i solidi e forme geometrichi che hanno un "interno" e "esterno" chiaro definito. I piu importanti oggetti di questo tipo sono: "box", "sphere", "cylinder", "cone", "torus", "prism". Un piano "plane" debbe essere considerato specialmente: Il vettore normale indica sempre al "esterno" del piano, mentre ogni punto dietro questo piano al altro lato di questo "plane" e definito come "interno".
Anche i mesh triangolari (mesh, mesh2) si può usare con queste operazioni, a condizione che c'è un inside_vector.
Tutte le operazioni csg si può combinare liberamente.
Le operazioni CSG sono nel dettaglio: