With the trace function of POV-Ray we are able to calculate the coordinates of a point of intersection of a straight line with any other object. For this we should define this object by "#declare". Then we can get the point of intersection by
trace ( Object, Start_Point, Trace_Direction );

Sample:
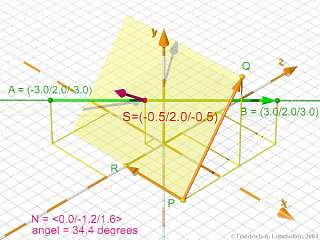
Point of Intersection of Line AB with a Plane
The plane here is defined by it's normalvector and a start point.

// points A and B of the line:
#declare A  = < 3.0, 1.0,-3.0>;
#declare B  = <-1.0, 3.0, 5.0>;

// plane
// normal vector:
#declare N = < 1, 0, -1>;
// start point:
#declare P = < 0.0, 0.0, 0.0>;

#declare Plane_1 =
object{
 Plane_NoP(  N, P, <-3,0,-4>,<2.5,4,4> )
 pigment{ color rgbt< 0.75,0.65,0.5,0.4> }
 }// end of Plane_1

// drawing the Plane_1:
 object{ Plane_1}

// point of intersection - Schnittpunkt
#declare Hit_the_Object =  trace ( Plane_1, A, B-A );

// showing the point of intersection:
sphere{ Hit_the_Object, Rp  pigment{ color Red } }
// showing it's relative position:
object{ Show_Yxz( Hit_the_Object, Rl/2)
        pigment{ color Yellow }}

For the output of the coordinates we use the built-in text object of POV-Ray:

text{ ttf "ARIAL.TTF"
  concat( "S = (",
           vstr(3, Hit_the_Object, "/", 0, 1),
          ")"
         ),0.1,0
  scale 0.40 rotate<20,-45,0>
  translate Hit_the_Object+< 0.4,0.0,0>
  pigment{ color Red }  no_shadow }

Normal vector at the point of intersection:
(useful for calculating the intersection angle!)
To get the coordinates of a normal vector in the point of intersection we need to prepare a place to store it's values:

#declare Hit_Normal = <0,0,0>;

Note: If the POV-Ray trace function does not find a point of intersection then the normal vector (here: Hit_Normal) remains the zero vector <0,0,0>
Checking this normal vector is the only reliable method to check whether an intersection took place or not!

#declare Hit_the_Object =
   trace ( Plane_1, A, B-A, Hit_Normal );

// The point of intersection - Schnittpunkt
 sphere{ Hit_the_Object, Rp  pigment{ color Red } }

// The normal vector at the point of intersection
object{ Vector( Hit_the_Object,
                Hit_the_Object + Hit_Normal, Rl)
        pigment{ color rgb<1,0,0.25>}
      }

Point of intersection of line and plane.

Click here for a complete description
of this scene for POV-Ray:
".txt" file or ".pov" file

Point of intersection of line and plane.

Click here for a complete description
of this scene for POV-Ray:
".txt" file or ".pov" file

Point of intersection of line and plane.

Click here for a complete description
of this scene for POV-Ray:
".txt" file or ".pov" file

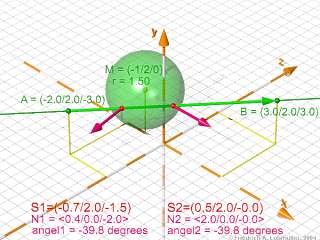
Point of Intersection of Line AB with a Sphere
As a simplification we take for granted that the hit the sphere.
Here we declare a sphere object and two intersection normals:

  // Sphere:
#declare M  = < -1, 2.0, 0.0>;
#declare Radius = 1.5 ;

// Sphere
#declare Sphere_1 =
sphere{ o, Radius
        translate M
        pigment{ color Green  transmit 0.5}
      }

// drawing the sphere
object{ Sphere_1}

// preparing the normal vectors
#declare Hit_Normal = <0,0,0>;
#declare Hit_Normal2 = <0,0,0>;

Then we trace the line from two direction against the sphere to get both points and normals of the intersections with the sphere:

#declare Hit_the_Object =
   trace ( Sphere_1, A, B-A, Hit_Normal );
#declare Hit_the_Object2 =
   trace ( Sphere_1, B, A-B, Hit_Normal2);

Point of intersection of line and plane.

Click here for a complete description
of this scene for POV-Ray:
".txt" file or ".pov" file