plane (semispace)
general syntax:
plane{< 0,1,0 >,0
rotate<0,0,0;>
translate<0,0,0;>
texture{ ... }
}// ----------------- |
|
Here "< 0,1,0 >" descripes the surface normal vector
of an infinite plane and the there following number < , , >, 0
discripes the distance to the origin in the direction of the normal vector.
Attention:
The distance is messured in direction of the surface normal vector
(attention to the sign!) and ony if the surface normal vector has a leght of 1
(a normed normal vector!) the distance is messured correctly in the base units!
|
To change the position and orientation of the plane, we have to turn it by
"rotate< , , >" and
move it by "translate< , , >".
|
|
The Surface-Normal-Vector-Form of a Plane: |
|
|
The Form "plane{<a,b,c>,d ... }" is equivalent to the
equation of a plane in surface normal form as well known from analytic geometrie:
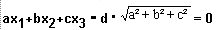
In this case this descripes - somehat different from analytic geometrie -
not only the points of an infinite plane, but also all points which are
behind this plane. Inside is opposite to the orientation of the surface normal vector.
The surface normal vector points to the "outside" of this "plane"
Stricktly speaking this "plane" discripes not only a plane but a whole semispace behind
(relatively to the surface normal vector) this plane.
The reason for this is: If a point is precisely in the plane,
is hardly decide for a computer because of it's inavoidable problems of accuracy
(rounding errors!) - that a point is definitely behind a plane is much easier to decide!
With this kind of objects and the boolean operations
(CSG) it is possible to modellizze new kind of bodies - i.e. the regular bodies
for crystal shapes like "Tetrahedron",
"Dodecahedron", "Icosahedron" etc., which are defined in
"shapes2.inc", they are builded in this way.
Tilled planes should be formed by basic planes. Because a surface normal vector
of a plane turned by 25° is difficult to calculate, it will be better to use
one of the coordinate planes and turn it by "rotate" and move it by
"translate" to bring it in it's final position and orientation.
|
Sample 1:
The plane
plane{<0.25,0.75,0>,
sqrt(1*1+3*3)
} // -------------- |
is easier to descripe by:
plane{ <1,3,0>,0
translate<1,3,0>
} // -------------- |
|
|
Sample 2:
The plane
plane{<-1,-1,0>,-sqrt(18)
} // -------------- |
is i.e.
identic with
plane{<2,2,0>,3*sqrt(2)
inverse
} // -------------- |
and it is easier to descripe by:
plane{<-1,0,0>, 0
rotate< 0, 0, -45>
translate<3,3,0>
} // -------------- |
|
|
|