plane (semispace)
syntaxe générale :
plane{< 0,1,0 >,0
rotate<0,0,0>
translate<0,0,0>
texture{ ... }
}// ---------- |
|
Ceci "< 0,1,0 >" décrit le vecteur normal de surface d'un plan
infini et le nombre suivant < , , >, 0 définie la distance de l'origine dans
la direction du vecteur à la normale.
Attention:
La distance est mesurée en direction du vecteur normal de surface (attention au signe !)
et aucun si le vecteur normal de surface a une longueur de 1 (vecteur normal normé ! )
la distance est mesurée correctement dans l'unité de base !
|
Pour changer la position et l'orientation du plan, il faut le
tourner avec "rotate< , , >"
et l'ôter avec "translate< , , >".
|
|
Le vecteur normal de surface : |
|
|
La Forme "plane{<a,b,c>,d ... }" est équivalente
à l'équation d'un plan de forme normale de surface réputée de la géométrie analytique :
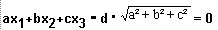
Dans ce cas ça décrit, un peu différement de la géométrie analytique,
non seulement les points d'un plan infini, mais ausi tous les points qui sont situés derrière ce plan.
L'intérieur est opposé à l'orientation du vecteur normal de surface. Le vecteur normal de
surface pointe vers l'extérieur de ce "plan"
Strictement parlant ce "plan" décrit non seulement un plan mais aussi tout le demi espace
derrière ce plan (relativement au vecteur normal à la surface) .
La raison en est : Si un point est précisement dans le plan, c'est difficile à juger
pour un ordinateur à cause des inévitables problèmes de précision
(arrondi des erreurs ! ) - Qu'un plan soit définitivement derrière est beaucoup plus facile à estimer !
Avec ce genre d'objets et les opération booléennes (CSG) il devient possible de
modéliser de nouvelles formes de corps. Par exemple le corps régulier pour les
formes de crystal telle que "Tetrahedron", "Dodecahedron",
"Icosahedron" etc., qui sont définis dans "shapes2.inc",
sont construites de cette façon.
Les plans creusés devraient être formés par des plans de base.
Parce-que un vecteur normal de surface d'un plan incliné de 25° est difficile
à calculer, c'est mieux d'utiliser un des plans de coordonnées et de l'incliner
par "rotate" et de le déplacer par "translate" pour l'amener
à sa position et à son orientation finales.
|
Exemple 1:
Le plan
plane{<0.25,0.75,0>,
sqrt(1*1+3*3)
} //----------------- |
est plus facile à décrire par :
plane{<1,3,0>,0
translate<1,3,0>
} //----------------- |
|
|
Exemple 2:
Le plan
plane{<-1,-1,0>,-sqrt(18)
} //----------------- |
est identique avec
plane{<2,2,0>,3*sqrt(2)
inverse
} //----------------- |
et plus facile à décrire par :
plane{<-1,0,0>, 0
rotate< 0, 0, -45>
translate<3,3,0>
} //----------------- |
|
|
|