"plane" - piano
(semi piano)

"plane" - piano
(semi piano)
Sintassi generale:

plane{< 0,1,0 >,0 rotate<0,0,0> translate<0,0,0> texture{ ... } }// ----------

Qui "< 0,1,0 >" descrive il vettore della normale sulla superficie del piano infinito e il numero dietro del vettore "< , , >, 0" descrive la distanza dell'origine nella direzione del vettore normale.
Attenzione:
La distanza è misurato nella direzione del vettore della normale (attenzione à segno!) e solo quando il vettore della normale ha la lunghezza di 1 (un vettore normale normalizzato!) la distanza è misurato corretto in unità di base!

Per cambiare la posizione e l'orientazione di un piano, dobbiamo tornarle con "rotate< , , >" e moverle con "translate< , , >".

Il vettore della normale alla superficie di un piano :

La forma
"plane{<a,b,c>,d ... }"
è equivalente all'equazione di un piano nella forma di un vettore della normale alla superficie del piano, ben conosciuto geometria a vettori classica:

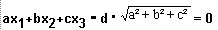
In questo caso l'equazione descrive - in una forma un poco diverso della geometria a vettori classica - non solo i punti di un piano infinito, ma anche tutti i punti che sono dietro questo piano. Interno è di fronte all'orientazione del vettore normale della superficie. Il vettore della normale alla superficie indica verso al di fuori del "piano"
A rigor di termini questo "piano" descrive non solo un piano ma un semi spazio completo dietro questo piano (relativo à il vettore della normale alla superficie del piano !).
Il motivo è questo: Se un punto si trova esattamente in un piano, è difficile a decidere per un computer, perchè problemi d'inesattezza sono inevitabile (rounding errors!) - se un punto è definitivamente dietro di un piano questo è molto più facile da decidere!
Con tutti questi tipi d'oggetti e l'operazione booleane (CSG) è possibile di modellare nuovi tipi di corpi - per esempio: forme regolare di tipo cristallo come "Tetrahedron", "Dodecahedron", "Icosahedron" etc. che sono definiti in "shapes2.inc" sono costrutto di questa maniera,
Piani inclinati si forma di piani elementari. Perchè il vettore della normale alla superficie di un piano inclinato con 25° è difficile a calcolare. è meglio di usare un piano di coordinate e d'inclinare questo piano con "rotate" e muoverle con "translate" per mettere il piano in posizione et in orientazione finale.

Esempio 1:
Il piano

plane{<0.25,0.75,0>,
        sqrt(1*1+3*3)
     } //-----------------

è piú facile a descrivere con:

plane{<1,3,0>,0
      translate<1,3,0>
     } //-----------------

Esempio 2:
Il piano

plane{<-1,-1,0>,-sqrt(18)
     } //-----------------

per essempio è identico con

plane{<2,2,0>,3*sqrt(2)
      inverse
     } //-----------------

et è piú facile a descrivere con:

plane{<-1,0,0>, 0
      rotate< 0, 0, -45>
      translate<3,3,0>
     } //-----------------

"plane" - piano(semi piano)

"plane" - piano
(semi piano)