|
|
plane = Ebene,
(eigentlich: Halbraum)
|
plane = Ebene
(eigentlich: Halbraum)
allgemeiner Syntax:
plane{ < 0,1,0 >,0
rotate<0,0,0>
translate<0,0,0>
texture{ ... }
}// ---------- |
|
Dabei beschreibt "< 0,1,0 >" den Normalenvektor der
"Ebene" und die darauffolgende Zahl den
Abstand der "Ebene" vom Koordinaten-Mittelpunkt an
- aber Vorsicht:
Der Abstand wird in Richtung des Normalenvektors berechnet (Vorzeichen beachten!) und
nur bei normierten Normalenvektoren (d.h. Normalenvektoren der Länge 1) wird
der Abstand in den jeweiligen Einheiten gemessen!
|
Will man eine andere Lage der Ebene erreichen, so empfiehlt es sich die Ebene mittels
"rotate< , , >"
und "translate< , , >"
in die gewünschte Position zu drehen und zu schieben.
|
Die Normalenform einer Ebene:
|
|
|
Der Form "plane{<a,b,c>,d ... }" entspricht in der
analytischen Geometrie die folgende wohlbekannte
Ebenengleichung in Normalenform:
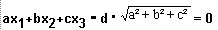
Beschrieben werden dadurch aber anders, als in der
analytischen Geometrie, nicht nur die Punkte auf der
Ebene, sondern auch alle Punkte, die auf derjenigen
Seite hinter der Ebene liegen, von welcher der
Normalenvektor wegzeigt.
Es wird also der gesamte
Halbraum hinter der Ebene dadurch bezeichnet,
wobei der Normalenvektor in den Außenraum zeigt!
Der Grund dafür liegt darin: Ob ein Punkt genau auf der Ebene liegt,
läßt sich für einen Computer aufgrund der unvermeidlichen
Rundungsfehler meist nicht sicher feststellen - daß ein Punkt sicher hinter
einer Ebene liegt, dies ist da schon leichter zu entscheiden!
Dies erlaubt es nun mit diesen Objekten und den
booleschen Operationen (CSG) neue Körper zu
modellieren - beispielsweise wurden die reguläen
Körper für Kristallformen, wie "Tetrahedron",
"Dodecahedron", "Icosahedron" etc., welche in
"shapes2.inc" definiert sind, auf diese Weise
konstruiert.
Die "Ebene" plane{<0,1,0>,0 ...} bezeichnet also
nicht etwa nur die xz-Ebene, sondern den gesamten
(relativ zur Richtung des Normalenvektors) hinter ihr liegenden Halbraum.
Schrägliegende Ebenen mit einem ungeradzahligem
Abstand vom Ursprung sollten aus Grundebenen
modelliert werden. Da ein Normalenvektor für eine
Ebene, welche um z.B. 25° gegen eine die
xz-Koordinatenebene geneigt ist nur schwer zu
berechnen ist, sollte man hierzu nur einfache
Grundebenen, wie z.B. die xz-Ebene verwenden, und
diese durch "rotate" und evtl. "translate" in ihre
genaue Lage bringen.
|
Beispiel 1:
Die Ebene
plane{ <0.25,0.75,0>,
sqrt(1*1+3*3)
} //----------------- |
läßt sich einfacher beschreiben durch:
plane{ <1,3,0>,0
translate<1,3,0>
} //----------------- |
|
|
Beispiel 2:
Die Ebene
plane{ <-1,-1,0>,-sqrt(18)
} //----------------- |
ist z.B.
identisch mit
plane{ <2,2,0>,3*sqrt(2)
inverse
} //----------------- |
läßt sich einfacher beschreiben durch:
plane{ <-1,0,0>, 0
rotate< 0, 0, -45>
translate<3,3,0>
} //----------------- |
|
|
|