Home
- 3D Animations Gallery
- POV-Ray Tutorial
3D Animation Tutorial
Index of Content
0. Basic Knowledge
1. Basic Example
2. Example 2
3. Images to Animated Gif
4. From Images to Video
5. Basic Terms
6. Animation Commands
I. Cyclic Animations
1. Rotating Objects
1.2. Planets in Orbit
1.3. Clock Animation
2. Rotating Camera
2.1. Straight Moving Camera
3. Western Wheel
Problem
3.1. Rolling Wheels
4. Gears
4.1. Roller Chain
4.2. Bike Chain
5. Swinging Pendulum
5.1. Newton's Cradle
5.2: Rock the Rocker
6. Spiral Pendulum
7. Coupling Rods
7.1. Connecting Rods
8. Psychedelic + Op-Art
9. Counters + Countdowns
10. Folding of a Cube
II. Non-linear Movements
1.0 Speed Up/Slow 0Down 1
> 1.1 Speed Up/Slow Down 2
2. Fall + Bounce
3. Acceleration by
physical Formulas
4. Speed Controll by
Spline Functions
III. Animation Paths
with Spline Curves
1. Spline Curves
2. Closed Splines
3. Animation Paths
|
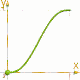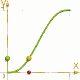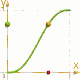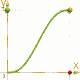 |
Speed Up and Slow Down (2)
Realistic nonlinear movements with useful basic functions. |
A more Realistic Simulation of
Acceleration and Retardation
with start and end at v = 0
and a = 0.
With an approximation by
f(x)= (0.5-0.5*cos( pi*x)) or
f(x)= - 2*x3+ 3*x2
we have f(0) = 0, f(1) = 1
and f'(0)=f'(1)=0.
For a movement starting and ending with v = 0 and a = 0,
we should use a function,
which not only have the 1st deviation with f'(0)=0 (start) and f'(1)=0 (end).
We need a function with also the
2nd deviation f''(0) = f''(1) = 0, like
f(x) = 6x5 - 15x4 + 10x3 =
f(x) = x⋅x⋅x⋅(10+x⋅(6⋅x-15))
The difference is obvious in the opposite image.
|
f(X)= 3*X*X - 2*X*X*X [orange] and
f(X)= X*X*X*(10+X*(6*X-15)) [green]
|
4 useful macros:
//---------------------------
#macro Smoothy_01 ( X )
X*X*X*(10+X*(6*X-15))
#end
//---------------------------
#macro Smoothy_010 ( X )
#if( X <= 0.5 )
(X*2)*(X*2)*(X*2)
*(10+(X*2)*(6*(X*2)-15))
#else
1-((X*2-1)*(X*2-1)*(X*2-1)
*(10+(X*2-1)*(6*(X*2-1)-15)))
#end
#end
//---------------------------
#macro Smoothy_10 ( X )
1-X*X*X*(10+X*(6*X-15))
#end
//---------------------------
#macro Smoothy_101( X )
#if( X <= 0.5 )
1-((X*2)*(X*2)*(X*2)
*(10+(X*2)*(6*(X*2)-15)))
#else
(X*2-1)*(X*2-1)*(X*2-1)
*(10+(X*2-1)*(6*(X*2-1)-15))
#end
#end
//--------------------------- |
|
macro 'smoothy01( TIME )'
Start smooth, end smooth.
macro 'smoothy10( TIME )'
Start smooth, end smooth.
|
macro 'smoothy010( TIME )'
Start smooth, return smooth,
come back and end smooth.
macro 'smoothy101( TIME )'
Start smooth, return smooth,
come back and end smooth.
|
|
Calculation of a polynomial function of the 5th degree:
We seek a function with f(0)=0 and f(1) = 1 and
the 1st and 2nd deviation = 0 at <0/0> and <1/1>.
General form:
f(x) = a⋅x5 + b⋅x4 + c⋅x3 + d⋅x2 + e⋅x + f
1st deviation:
f'(x) = 5⋅a⋅x4 + 4⋅b⋅x3 + 3⋅c⋅x2 + 2⋅d⋅x + e
2nd deviation:
f''(x) = 20⋅a⋅x3 + 12⋅b⋅x2 + 6⋅c⋅x + 2⋅d
Conditions at point <0/0>:
f(0) = 0, f'(0) = 0, f''(0) = 0;
Therfore we get: f = 0, e = 0 and d = 0.
Reduced general forms:
f(x) = a⋅x5 + b⋅x4 + c*x3
f'(x) = 5⋅a⋅x4 + 4⋅b⋅x3 + 3⋅c⋅x2
f''(x) = 20⋅a⋅x3 + 12⋅b⋅x2 + 6⋅c⋅x
Conditions at point <1/1>:
f(1) = 1, f'(1) = 0, f''(1) = 0;
f(1) = a + b + c = 1 (I)
f'(1) = 5⋅a + 4⋅b + 3⋅c = 0 (II)
f''(1) = 20⋅a + 12⋅b + 6⋅c = 0 (III)
II : 5a + 4b +3c = 0
-3⋅I: -3a - 3b - 3c = -3
=> 2a + b = -3 (IV)
II : 5a + 4b + 3c = 0
III/2 : 10a + 6b + 3c = 0
=> 5a + 2b = 0 (V)
-2⋅IV : -4a - 2b = 6
V : 5a + 2b = 0
=> a = 6
a in IV : 12 + b = -3
b = -15
a,b in I: 6 - 15 + c = 1
-9 + c = 1
c = 10
The resulting function is
f(x) = 6⋅x5 - 15⋅x4 + 10⋅x3
|
|