Home
- Galeria Animazione 3D
- Tutorial POV-Ray
Animazione 3D
Indice del contenuto
0. Nozioni fondamentali
1. Esempio di base
2. Esempio 2
3. Da Immagini al animated gif
4. Da Immagini al Video
5. Termini tecnici di base
6. Comandi di Animazione
I. Animazioni ciclici
1. Oggetti rotanti
1.2. Pianeti in orbita
1.3. L'Orologio
2. Fotocamera rotante
2.1. Fotocamera in volo dritto
3. Il Problema di
Ruota Western
3.1. Ruote Girante
4. Ingranaggi
4.1. Catena di Trasmissione
4.2. Catena della Bicicletta
5. Pendolo oscillante
5.1. Pendolo di Newton
5.2. Rock il Rocking Chair!
6. Molla a spirale
7. Biella di accoppiamento
7.1. Biella motrice
8. Psychedelico + Op-Art
9. Contatori + Countdown
10. Piegatura di un Cubo
II. Movimenti non-lineari
1.0 Accelerare e Frenare 1
> 1.1 Accelerare e Frenare 2
2. Cadere e Saltellare
3. Accelerazione secondo
le formule de la fisica
4. Controllo di movimenti
con funzioni spline
III. Sentieri di Animazione
con Spline
1. Curve Spline
2. Spline ciuso
3. Sentieri di Animazione
|
 |
Accelerare e Frenare (2)
Mouvementi non lineari in animazioni per l'accelerazione e per la decelerazione realistica con funzioni di base in POV-Ray. |
|
Simulazione plus realistica di
accelerazione e decelerazione
con inizio e fine con v = 0 e a = 0.
Con una approssimazione con
f(x)= (0.5-0.5*cos( pi*x)) o
f(x)= - 2*x3+ 3*x2
abbiamo f(0) = 0, f(1) = 1
e f'(0) = f'(1) = 0.
Per un movimento con inizio e fine con v = 0 e a = 0,
dobbiamo utilisare una funzione,
che non ha solamente la derivazione prima
f'(0)=0 (inizio) e f'(1)=0 (fine).
Abbiamo besogno di una funzione con anche la derivazione seconda
f''(0) = f''(1) = 0, come
f(x) = 6x5 - 15x4 + 10x3 =
f(x) = x⋅x⋅x⋅(10+x⋅(6⋅x-15))
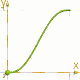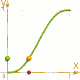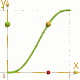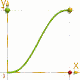
La differenza è ovviamente nella illustrazione adiacente.
|
f(X)= 3*X*X - 2*X*X*X [arancio] e
f(X)= X*X*X*(10+X*(6*X-15)) [verde]
|
4 macro utili:
//---------------------------
#macro Smoothy_01 ( X )
X*X*X*(10+X*(6*X-15))
#end
//---------------------------
#macro Smoothy_010 ( X )
#if( X <= 0.5 )
(X*2)*(X*2)*(X*2)
*(10+(X*2)*(6*(X*2)-15))
#else
1-((X*2-1)*(X*2-1)*(X*2-1)
*(10+(X*2-1)*(6*(X*2-1)-15)))
#end
#end
//---------------------------
#macro Smoothy_10 ( X )
1-X*X*X*(10+X*(6*X-15))
#end
//---------------------------
#macro Smoothy_101( X )
#if( X <= 0.5 )
1-((X*2)*(X*2)*(X*2)
*(10+(X*2)*(6*(X*2)-15)))
#else
(X*2-1)*(X*2-1)*(X*2-1)
*(10+(X*2-1)*(6*(X*2-1)-15))
#end
#end
//--------------------------- |
|
macro 'smoothy01( TIME )'
Start smooth, end smooth.
macro 'smoothy10( TIME )'
Start smooth, end smooth.
|
macro 'smoothy010( TIME )'
Start smooth, return smooth,
come back and end smooth.
macro 'smoothy101( TIME )'
Start smooth, return smooth,
come back and end smooth.
|
|
Calculazione di una funzione polinomiale de quinto grado:
Cerchiamo una funzione con f(0)=0 e f(1) = 1 e
la derivazione prima e seconda = 0 a <0/0> e <1/1>.
Forma generale:
f(x) = a⋅x5 + b⋅x4 + c⋅x3 + d⋅x2 + e⋅x + f
derivazione prima:
f'(x) = 5⋅a⋅x4 + 4⋅b⋅x3 + 3⋅c⋅x2 + 2⋅d⋅x + e
derivazione seconda:
f''(x) = 20⋅a⋅x3 + 12⋅b⋅x2 + 6⋅c⋅x + 2⋅d
Condizioni al puntot <0/0>:
f(0) = 0, f'(0) = 0, f''(0) = 0;
Con questa abbiamo: f = 0, e = 0 et d = 0.
Forma generale ridotto:
f(x) = a⋅x5 + b⋅x4 + c*x3
f'(x) = 5⋅a⋅x4 + 4⋅b⋅x3 + 3⋅c⋅x2
f''(x) = 20⋅a⋅x3 + 12⋅b⋅x2 + 6⋅c⋅x
Condizioni al punto <1/1>:
f(1) = 1, f'(1) = 0, f''(1) = 0;
f(1) = a + b + c = 1 (I)
f'(1) = 5⋅a + 4⋅b + 3⋅c = 0 (II)
f''(1) = 20⋅a + 12⋅b + 6⋅c = 0 (III)
II : 5a + 4b +3c = 0
-3⋅I: -3a - 3b - 3c = -3
=> 2a + b = -3 (IV)
II : 5a + 4b + 3c = 0
III/2 : 10a + 6b + 3c = 0
=> 5a + 2b = 0 (V)
-2⋅IV : -4a - 2b = 6
V : 5a + 2b = 0
=> a = 6
a in IV : 12 + b = -3
b = -15
a,b in I: 6 - 15 + c = 1
-9 + c = 1
c = 10
Il resultato e la funczione
f(x) = 6⋅x5 - 15⋅x4 + 10⋅x3
|
|