Home
- Tutorial POV-Ray
- Geometria di Base
per Raytracing
Triangolo Rettangolo
Teorema di Pitagora
Trigonometria di Base
Teorema del Coseno
Triangolo Equilatero
Poligono Regulare
Poliedro
Tetraedro Regolare
Ottaedro Regolare
Cubo e Cuboide
Dodecaedro Regolare
Icosaedro Regolare
Cubottaedro
Ottaedro troncato
Rombicubottaedro
Icosaedro troncato
Cerchi
Cerchi tangenti
Tangenti interne
Tangenti esterne
- Animazioni Geometriche 3D
|
Teorema del Coseno
Qualche fondamento geometrico molto utile
su gli angoli e i lati di triangoli. |
Nota: Per le funzioni trigonometriche sin(X), cos(X) and tan(X) in POV-Ray
dobbiamo avere il argumento X espresso in radianti !!!
I funzioni inverse asin(x), acos(x) e atan(x) danno gli angoli in radianti !
|
Per ogni tiangolo ABC :
c2 = a2 + b2 - 2*a*b*cos( γ ) (1)
b2 = a2 + c2 - 2*a*c*cos( β ) (2)
a2 = b2 + c2 - 2*b*c*cos( α ) (3)
Per γ = 90° = pi/2 (triangolo rettangolo)
è cos(γ) = 0 e cosi con (1):
c2 = a2 + b2 (Teorema di Pitagora).
-----------------------------------------------------
Per gli angoli di un triangolo ABC
ciò conduce alle seguente formule:
γ = acos ( ( a2 + b2 - c2 )/(2*a*b) ) (4)
β = acos ( ( a2 + c2 - b2 )/ (2*a*c) ) (5)
α = acos ( ( b2 + c2 - a2 )/ (2*b*c) ) (6)
|
|
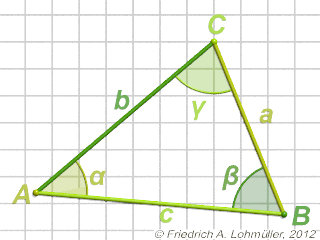
Un triangolo ABC in 2D.
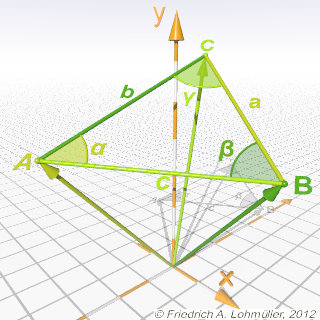
Un triangolo ABC in 3D.
|
|
|
|