Forme Polynomiali = forme rapresentate con equazioni polynomiali
built-in objects
Equazioni polynomiali sono la base di tutte le forme nello spazio 3D.
Qualche forma frequentemente usata come piano ("plane"), sfera ("sphere"),
cylindro("cylinder"), cono ("cone"), toro ("torus")
sono disponibile in POV-Ray con commandi amichevoli,
anche per gente qui non sono amici intimi della matematica.
Ma con equazioni polynomiali é possibile di descrivere anche altri tipi di superfici
come Lemniscate, Devils curve, Monkey saddle, Piriform, Steiner surface.
POV-Ray tene a disposizione 3 oggetti differenti per creare superfici
directamente con equazioni polynomiali:
"cubic{ ... }", "quartic{ ... }" e "poly{ ... }".
Un excursus breve sopra equazioni polynomiali
Superfici polynomiali di primo grado
(ogni termine contiene solo x, y o z in forma lineare.)
Ogni superficie polynomiale di primo grado si può rappresentare con un'equazione
a*x + b*y + c*z - d*sqrt(a2 + b2 + c2) = 0.
Esempio: 0*x + 1*y + 1*z - 2 = 0
plane { <0, 1, 1>, 2 }
Superfici polynomiali di secondo grado
Una superficie polynomiale di secondo grado ha un'equazione quadrica, un'equazione di secondo grado
que posso anche contenere termini come x2, y2, z2, xy, xz e yz.
Per esempio: sfere si può definire con equazioni quadriche.
Una sfera intorno al centro M = <mx, mym, z>
ha l'equazione:
(x - mx)2
+ (y - my)2
+ (z - mz)2
- r2 = 0
<=>
x2 - 2*mx*x + mx2
+ y2 - 2*my*y + my2
+ z2 - 2*mz*z + mz2
- r2 = 0
<=>
x2 + (- 2*mx)*x
+ y2 + (- 2*my)*y
+ z2 + (- 2*mz)*z
+ ( mx2
+ my2
+ mz2
- r2) = 0
Esempio: Una sfera intorno a <3, 4, 0> con raggio 5
si può di descrivere con un'equazione quadrica
x2 + (- 2*3)*x
+ y2 + (- 2*4)*y
+ z2 + (- 2*0)*z
+ ( 32
+ 42
+ 02
- 52) = 0
<=>
x2 - 6*x
+ y2 - 8*y
+ z2
= 0
La equazione quadrica generale ha 10 coefficienti a1, a2, ... a10:
a1*x2 + a2*xy + a3*xz + a4*x
+ a5*y2 + a6*yz + a7*y + a8*z2 + a9*z + a10*1 = 0.
Syntax sample:
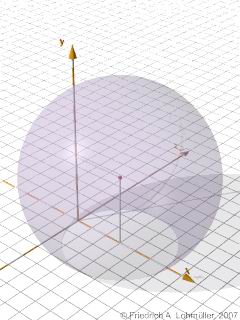 |
// --- polynomial surface ------------
poly{ 2,
<1, 0, 0, -6, 1, 0, -8, 1, 0, 0>
// sturm
texture{
pigment{ color rgbt<0.8,0.6,1,0.7>}
finish { phong 0.2 }
}
scale 1
rotate <0, 0, 0>
translate < 0, 0, 0>
} // end of polynomial surface -------
// sphere oggetto equivalente:
sphere{ <3,4,0>, 5
...
} //-------------- |
Superfici polynomiali sono descritte
con un'equazione di primo grado (planes) con 4 coefficienti,
con un'equazione di secondo grado (i.e. sfere, ellipsoidi, cylindri, coni) con 10 coefficienti,
o con ...
|
3. grado
cubic equations
20 coefficienti
// --- cubic surface ---
cubic{
< a1, a2, a3,...,a20>
// sturm
... // modifiers
} // end of cubic |
4. grador
quartic equations
35 coefficienti
// --- quartic surface -
quartic{
< a1, a2, a3,...,a20>
// sturm
... // modifiers
} // end of quartic |
5. grado - 56 coefficienti
o più alto
vede POV-Ray help!
// polynomial surface -
poly{ Order,
< a1, a2, a3,...,an>
// sturm
... // modifiers
} // end of polynomial |
Una esempio per una superficie "quartic":
Un toro con raggio majore r0, raggio minore r1 si può discrivere
con un'equazione di secondo grado:
x4
+ y4
+ z4
+ 2*x2*y2
+ 2*x2*z2
+ 2*y2*z2
- 2*(r0+r1)*x2
+ 2*(r0-r1)*y2
- 2*(r0+r1)*z2
+ (r0-r1)2 = 0
La stessa equazione assortato in ordine di x, y, z per sintassi POV-Ray di "quatric":
1*x4
+ 0*x3*y
+ 0*x3*z
+ 0*x3
+ 2*x2*y2
+ 0*x2*y*z
+ 0*x2*y
+ 2*x2*z2
+ 0*x2*z
- 2*(r0+r1)*x2
+ 0*x*y3
+ 0*x*y2*z
+ 0*x*y2
+ 0*x*y*z2
+ 0*x*y*z
+ 0*x*y
+ 0*x*z3
+ 0*x*z2
+ 0*x*z
+ 0*x
+ 1*y4
+ 0*y3*z
+ 0*y3
+ 2*y2*z2
+ 0*y2*z
+ 2*(r0-r1)*y2
+ 0*y*z3
+ 0*y*z2
+ 0*y*z
+ 0*y
+ 1*z4
- 0*z3
- 2*(r0+r1)*z2
- 0*z
+ (r0-r1)2*1 = 0
// Torus con raggio majore sqrt(40), raggio minore sqrt(12)
quartic {
< 1, 0, 0, 0, 2, 0, 0, 2, 0, -104,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
1, 0, 0, 2, 0, 56, 0, 0, 0, 0,
1, 0, -104, 0, 784 >
sturm
} // ------------------------------------------------- |
// più corto con oggetto torus equivalente:
torus{ sqrt(40), sqrt(12)
} //------------------ |
Questo esempio di "torus" si è anche descritto nel include file "shapesq.inc":
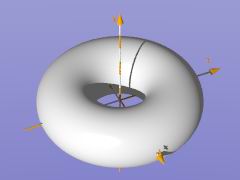 |
object{ Torus_40_12 //---------------
sturm
texture{
pigment{ color rgb<1,1,1>}
finish { phong 1}
}
rotate<0,0,0>
scale <1,1,1>*0.125
translate <0,0,0>
} // ----------- end of object |
|
Più superfici non-trivali con cubic, quartic e altri forme polynomiali
de include file "shapesq.inc":
si può vedere qui.
|
|