Polynomial shapes = shapes which are defined by polynomial equations
built-in objects
Polynomial equations are the base of all shapes in the 3d space.
Some often used shapes like plane, sphere, cylinder, cone, torus are available in POV-Ray
also to people which aren's too familiar with mathematics by their own user-friendly statements.
But with polynomial equations it's possible to descripe much more kind of surfaces like the
Lemniscate, Devils curve, Monkey saddle, Piriform, Steiner surface.
POV-Ray provides 3 different objects to create surfaces directly by polynomial equations:
"cubic{ ... }", "quartic{ ... }" and "poly{ ... }".
A short excursus on polynomial equations
First order polynomial shapes
(each term contains only single powers of x, y or z.)
Each polynomial shape of first order can be represented by the equation
A*x + B*y + C*z - D*sqrt(A2 + B2 + C2) = 0.
Example: 0*x + 1*y + 1*z - 2 = 0
plane { <0, 1, 1>, 2 }
Second order polynomial shapes
A second order polynomial shape has a quadric equation which also contains
terms like x2, y2, z2, xy, xz and yz.
I.e.: spheres can be defined by quadric equations.
A sphere around center M = <mx, mym, z> :
(x - mx)2
+ (y - my)2
+ (z - mz)2
- r2 = 0
<=>
x2 - 2*mx*x + mx2
+ y2 - 2*my*y + my2
+ z2 - 2*mz*z + mz2
- r2 = 0
<=>
x2 + (- 2*mx)*x
+ y2 + (- 2*my)*y
+ z2 + (- 2*mz)*z
+ ( mx2
+ my2
+ mz2
- r2) = 0
Sample: A sphere around <3, 4, 0> with radius 5
can be descriped by the quadric equation
x2 + (- 2*3)*x
+ y2 + (- 2*4)*y
+ z2 + (- 2*0)*z
+ ( 32
+ 42
+ 02
- 52) = 0
<=>
x2 - 6*x
+ y2 - 8*y
+ z2
= 0
A general quadric equation has 10 coefficients A1, A2, ... A10:
A1*x2 + A2*xy + A3*xz + A4*x
+ A5*y2 + A6*yz + A7*y + A8*z2 + A9*z + A10*1 = 0.
Syntax sample:
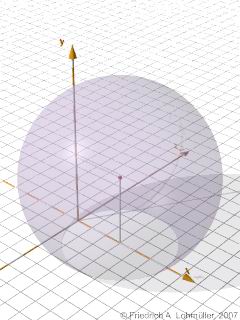 |
// --- polynomial surface ------------
poly{ 2,
<1, 0, 0, -6, 1, 0, -8, 1, 0, 0>
// sturm
texture{
pigment{ color rgbt<0.8,0.6,1,0.7>}
finish { phong 0.2 }
}
scale 1
rotate <0, 0, 0>
translate < 0, 0, 0>
} // end of polynomial surface -------
// equivalent sphere object:
sphere{ <3,4,0>, 5
...
} //-------------- |
Polynomial surfaces are descriped
by equations of first order(planes) with 4 coefficients,
by equations of second order (i.e. spheres, ellipsoids, cylinders, cones) with 10 coefficients,
or by ...
|
3rd order
cubic equations
20 coefficients
// --- cubic surface ---
cubic{
< A1, A2, A3,... A20>
// sturm
... // modifiers
} // end of cubic |
4th order
quartic equations
35 coefficients
// --- quartic surface -
quartic{
< A1, A2, A3,... A20>
// sturm
... // modifiers
} // end of quartic |
5th order - 56 coefficients
or higher order
see list in POV-Ray help!
// - polynomial surface
poly{ Order,
< A1, A2, A3,... An>
// sturm
... // modifiers
} // end of polynomial |
A Quartic Surface Sample:
A torus with major radius r0, minor radius r1 can be descriped by
a quartic equation:
x4
+ y4
+ z4
+ 2*x2*y2
+ 2*x2*z2
+ 2*y2*z2
- 2*(r0+r1)*x2
+ 2*(r0-r1)*y2
- 2*(r0+r1)*z2
+ (r0-r1)2 = 0
Same equation sorted by x, y, z for POV-Ray syntax of "quatric":
1*x4
+ 0*x3*y
+ 0*x3*z
+ 0*x3
+ 2*x2*y2
+ 0*x2*y*z
+ 0*x2*y
+ 2*x2*z2
+ 0*x2*z
- 2*(r0+r1)*x2
+ 0*x*y3
+ 0*x*y2*z
+ 0*x*y2
+ 0*x*y*z2
+ 0*x*y*z
+ 0*x*y
+ 0*x*z3
+ 0*x*z2
+ 0*x*z
+ 0*x
+ 1*y4
+ 0*y3*z
+ 0*y3
+ 2*y2*z2
+ 0*y2*z
+ 2*(r0-r1)*y2
+ 0*y*z3
+ 0*y*z2
+ 0*y*z
+ 0*y
+ 1*z4
- 0*z3
- 2*(r0+r1)*z2
- 0*z
+ (r0-r1)2*1 = 0
// Torus with major radius sqrt(40), minor radius sqrt(12)
quartic {
< 1, 0, 0, 0, 2, 0, 0, 2, 0, -104,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
1, 0, 0, 2, 0, 56, 0, 0, 0, 0,
1, 0, -104, 0, 784 >
sturm
} // ------------------------------------------------- |
// shorter with equivalent torus object:
torus{ sqrt(40), sqrt(12)
} //------------------ |
This sample torus is also descriped in the include file "shapesq.inc":
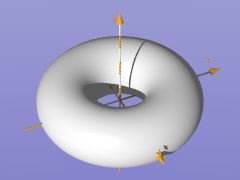 |
object{ Torus_40_12 //---------------
sturm
texture{
pigment{ color rgb<1,1,1>}
finish { phong 1}
}
rotate<0,0,0>
scale <1,1,1>*0.125
translate <0,0,0>
} // ----------- end of object |
|
More non trival cubic, quartic and other polynomial shapes
from the include file "shapesq.inc":
you can see here.
|