Formes de polynômes = formes représentées avec équations de polynômes
built-in objects
Èquations de polynôme sont la base de tous les formes dans l'espace 3D.
Quelques formes fréquemment utiliser, comme plan ("plane"), sphère ("sphere"),
cylindre ("cylinder"), cône ("cone"), tore ("torus")
sont disponible en POV-Ray avec des commandes conviviales,
aussi pour tous ces gens que ne sont pas amis intimes des mathématiques transcendantes.
Mais avec équations de polynômes il est possible de décrire aussi plus autres types de surfaces
comme Lemniscate, Devils curve, Monkey saddle, Piriform, Steiner surface.
En POV-Ray ils sont disponibel 3 objets différent pour créer surfaces
directement avec équations de polynômes :
"cubic{ ... }", "quartic{ ... }" et "poly{ ... }".
Un'excursion brève sur sopra équations de polynômes
Surfaces de polynômes du premier degré
(chaque terme contient seulement x, y ou z en forme linéaire.)
Chaque surfaces de polynômes du premier degré on peut représenter avec une equation du second degré
a*x + b*y + c*z - d*sqrt(a2 + b2 + c2) = 0.
Exemple: 0*x + 1*y + 1*z - 2 = 0
plane { <0, 1, 1>, 2 }
Surfaces de polynômes du second degré
Une surfaces de polynômes du second degré a une equation du second degré
que peut aussi contenir termes comme x2, y2, z2, xy, xz ou/et yz.
Par exemple : une sphère on peut définir avec une equation du second degré.
Une sphère autour le centre M = <mx, mym, z>
a l'equation:
(x - mx)2
+ (y - my)2
+ (z - mz)2
- r2 = 0
<=>
x2 - 2*mx*x + mx2
+ y2 - 2*my*y + my2
+ z2 - 2*mz*z + mz2
- r2 = 0
<=>
x2 + (- 2*mx)*x
+ y2 + (- 2*my)*y
+ z2 + (- 2*mz)*z
+ ( mx2
+ my2
+ mz2
- r2) = 0
Exemple : Une sphère autour de <3, 4, 0> avec rayon 5
on peut décrire avec une equation du second degré
x2 + (- 2*3)*x
+ y2 + (- 2*4)*y
+ z2 + (- 2*0)*z
+ ( 32
+ 42
+ 02
- 52) = 0
<=>
x2 - 6*x
+ y2 - 8*y
+ z2
= 0
Une equation du second degré généralement a 10 coefficients a1, a2, ... a10:
a1*x2 + a2*xy + a3*xz + a4*x
+ a5*y2 + a6*yz + a7*y + a8*z2 + a9*z + a10*1 = 0.
Example de syntaxe :
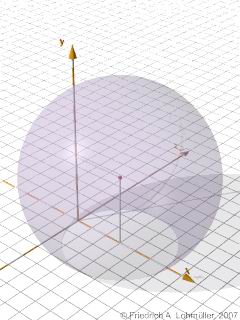 |
// --- polynomial surface ------------
poly{ 2,
<1, 0, 0, -6, 1, 0, -8, 1, 0, 0>
// sturm
texture{
pigment{ color rgbt<0.8,0.6,1,0.7>}
finish { phong 0.2 }
}
scale 1
rotate <0, 0, 0>
translate < 0, 0, 0>
} // end of polynomial surface -------
// objet de sphère equivalent:
sphere{ <3,4,0>, 5
...
} //-------------- |
Superfici polynomiali sono descritte
avec une equatione du premier degré (plan) avec 4 coefficients,
avec une equation du second degré (par example : sphère, ellipsoide, cylindre, cône) avec 10 coefficients,
ou avec ...
|
3. degré
equations cubiques
20 coefficients
// --- cubic surface ---
cubic{
< a1, a2, a3,...,a20>
// sturm
... // modifiers
} // end of cubic |
4. degré
equations quartiques
35 coefficients
// --- quartic surface -
quartic{
< a1, a2, a3,...,a20>
// sturm
... // modifiers
} // end of quartic |
5. degré - 56 coefficients
ou plus 'haut
voyez POV-Ray help!
// polynomial surface -
poly{ Order,
< a1, a2, a3,...,an>
// sturm
... // modifiers
} // end of polynomial |
Une exemple pour une surface "quartic":
Un tore avec rayon majeur r0, rayon mineur r1 on peut décrire
avec une equation du second degré :
x4
+ y4
+ z4
+ 2*x2*y2
+ 2*x2*z2
+ 2*y2*z2
- 2*(r0+r1)*x2
+ 2*(r0-r1)*y2
- 2*(r0+r1)*z2
+ (r0-r1)2 = 0
La même equation sortée à tour de rôle de x, y, z pour le syntaxe de POV-Ray pour "quatric":
1*x4
+ 0*x3*y
+ 0*x3*z
+ 0*x3
+ 2*x2*y2
+ 0*x2*y*z
+ 0*x2*y
+ 2*x2*z2
+ 0*x2*z
- 2*(r0+r1)*x2
+ 0*x*y3
+ 0*x*y2*z
+ 0*x*y2
+ 0*x*y*z2
+ 0*x*y*z
+ 0*x*y
+ 0*x*z3
+ 0*x*z2
+ 0*x*z
+ 0*x
+ 1*y4
+ 0*y3*z
+ 0*y3
+ 2*y2*z2
+ 0*y2*z
+ 2*(r0-r1)*y2
+ 0*y*z3
+ 0*y*z2
+ 0*y*z
+ 0*y
+ 1*z4
- 0*z3
- 2*(r0+r1)*z2
- 0*z
+ (r0-r1)2*1 = 0
// Tore avec rayon majeur racine carrée de 40, rayon mineur racine carrée de 12
quartic {
< 1, 0, 0, 0, 2, 0, 0, 2, 0, -104,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
1, 0, 0, 2, 0, 56, 0, 0, 0, 0,
1, 0, -104, 0, 784 >
sturm
} // ------------------------------------------------- |
// plus court avec l'objet "torus" équivalent :
torus{ sqrt(40), sqrt(12)
} //------------------ |
Cet exemple de "torus" est aussi décrit dans le fichier include "shapesq.inc":
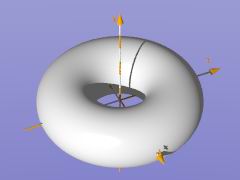 |
object{ Torus_40_12 //---------------
sturm
texture{
pigment{ color rgb<1,1,1>}
finish { phong 1}
}
rotate<0,0,0>
scale <1,1,1>*0.125
translate <0,0,0>
} // ----------- end of object |
|
Plus de surfaces non-trivale avec cubic, quartic et autre formes de polynômes
du fichier include "shapesq.inc":
si peut voir ici .
|
|