Polynomiale Oberflächen = Körperformen, welche durch polynomiale Gleichungen beschrieben werden können.
built-in objects
Polynomiale Gleichungen sind die Grundlage aller Körperformen im 3D-Raum.
Einige oft verwendete Formen wie Ebene(plane), Kugel(sphere), Zylinder(cylinder), Kegel(cone) oder Torus sind
in POV-Ray direkt über benutzerfreundliche Kommandos zugänglich - auch für Leute, die nicht
besonders gut mit der Mathematik vertraut sind.
Aber mit polynomialen Gleichungen lassen sich noch viel mehr Arten von Oberflächen beschreiben
wie etwa Lemniscate, Devils curve, Monkey saddle, Piriform, Steiner surface.
POV-Ray stellt 3 verschiedene Objekte bereit um berflächen direkt nach polynomialen Gleichungen zu erzeugen:
"cubic{ ... }", "quartic{ ... }" und "poly{ ... }".
Ein kleiner Exkurs in polynomiale Gleichungen
Polynomiale Flächen ersten Grades (First order polynomial shapes)
(jeder Term enhält nur linear x, y oder z.)
Polynomiale Flächen ersten Grades kann dargestellt werden durch die Gleichung
a*x + b*y + c*z - d*sqrt(a2 + b2 + c2) = 0.
Beispiel: 0*x + 1*y + 1*z - 2 = 0
plane { <0, 1, 1>, 2 }
Polynomiale Flächen zweiten Grades
Eine polynomiale Fläche zweiten Grades hat eine quadrische Gleichung, welche auch Terme enhält wie
x2, y2, z2, xy, xz und/oder yz.
Z.B.: Kugeln kann man mit quadrischen Gleichungen beschreiben.
Eine Kugel mit dem Zentrum M = <mx, mym, z> :
(x - mx)2
+ (y - my)2
+ (z - mz)2
- r2 = 0
<=>
x2 - 2*mx*x + mx2
+ y2 - 2*my*y + my2
+ z2 - 2*mz*z + mz2
- r2 = 0
<=>
x2 + (- 2*mx)*x
+ y2 + (- 2*my)*y
+ z2 + (- 2*mz)*z
+ ( mx2
+ my2
+ mz2
- r2) = 0
Beispiel: Eine Kugel um <3, 4, 0> mit Radius 5
kann beschrieben werden durch die quadrische Gleichung
x2 + (- 2*3)*x
+ y2 + (- 2*4)*y
+ z2 + (- 2*0)*z
+ ( 32
+ 42
+ 02
- 52) = 0
<=>
x2 - 6*x
+ y2 - 8*y
+ z2
= 0
Eine allgemeine quadrische Gleichung besitzt 10 Koeffizienten a1, a2, ... a10:
a1*x2 + a2*xy + a3*xz + a4*x
+ a5*y2 + a6*yz + a7*y + a8*z2 + a9*z + a10*1 = 0.
Syntax Beispiel:
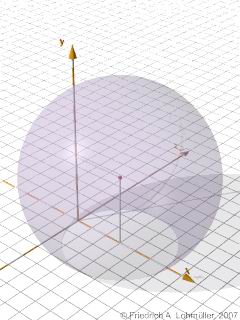 |
// --- polynomial surface ------------
poly{ 2,
<1, 0, 0, -6, 1, 0, -8, 1, 0, 0>
// sturm
texture{
pigment{ color rgbt<0.8,0.6,1,0.7>}
finish { phong 0.2 }
}
scale 1
rotate <0, 0, 0>
translate < 0, 0, 0>
} // end of polynomial surface -------
// ─quivalentes Sphere-Objekt:
sphere{ <3,4,0>, 5
...
} //-------------- |
Polynomiale Oberflächen werden beschrieben durch
Gleichungen ersten Grades (lineare Gleichungen, Ebenen, plane) mit 4 Koeffizienten,
Gleichungen zweiten Grades (quadratische Gln. z.B. Kugel, Ellipsoid, Zylinders, Kegel) mit 10 Koeffizienten,
or by ...
|
3. Grades
cubic - kubische Gleichungen
20 Koeffizienten
// --- cubic surface ---
cubic{
< a1, a2, a3,...,a20>
// sturm
... // modifiers
} // end of cubic |
4. Grades
quartic - Gleichungen 4.Grades
35 Koeffizienten
// --- quartic surface -
quartic{
< a1, a2, a3,...,a20>
// sturm
... // modifiers
} // end of quartic |
5. Grades - 56 Koeffizienten
oder höheren Grades
siehe Liste in
POV-Ray help!// polynomial surface
poly{ Grad,
< a1, a2, a3,...,an>
// sturm
... // modifiers
} // end of polynomial |
Ein Beispiel für eine Quartic-Oberfläche:
Ein Torus mit Radius major r0, Radius minor r1 kann durch folgende
Gleichung vierten Grades beschrieben werden:
x4
+ y4
+ z4
+ 2*x2*y2
+ 2*x2*z2
+ 2*y2*z2
- 2*(r0+r1)*x2
+ 2*(r0-r1)*y2
- 2*(r0+r1)*z2
+ (r0-r1)2 = 0
Diselbe Gleichung sortiert nach x, y, z für die POV-Ray Syntax von "quatric":
1*x4
+ 0*x3*y
+ 0*x3*z
+ 0*x3
+ 2*x2*y2
+ 0*x2*y*z
+ 0*x2*y
+ 2*x2*z2
+ 0*x2*z
- 2*(r0+r1)*x2
+ 0*x*y3
+ 0*x*y2*z
+ 0*x*y2
+ 0*x*y*z2
+ 0*x*y*z
+ 0*x*y
+ 0*x*z3
+ 0*x*z2
+ 0*x*z
+ 0*x
+ 1*y4
+ 0*y3*z
+ 0*y3
+ 2*y2*z2
+ 0*y2*z
+ 2*(r0-r1)*y2
+ 0*y*z3
+ 0*y*z2
+ 0*y*z
+ 0*y
+ 1*z4
- 0*z3
- 2*(r0+r1)*z2
- 0*z
+ (r0-r1)2*1 = 0
// Torus mit Radius major sqrt(40), Radius minor sqrt(12)
quartic {
< 1, 0, 0, 0, 2, 0, 0, 2, 0, -104,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
1, 0, 0, 2, 0, 56, 0, 0, 0, 0,
1, 0, -104, 0, 784 >
sturm
} // ------------------------------------------------- |
// kürzer mit dem äquivalenten Torus-Objekt:
torus{ sqrt(40), sqrt(12)
} //------------------ |
Dieses Torus-Beispiel wird auch in der Include-Datei "shapesq.inc" beschrieben:
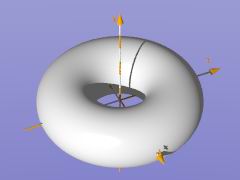 |
object{ Torus_40_12 //---------------
sturm
texture{
pigment{ color rgb<1,1,1>}
finish { phong 1}
}
rotate<0,0,0>
scale <1,1,1>*0.125
translate <0,0,0>
} // ----------- end of object |
|
Mehr nicht-trivale cubic, quartic und andere polynomiale Formen
aus der Include-Datei "shapesq.inc":
kann man hier sehen.
|