matrix < , , >
Matrici e Corrispondenza Affine
La parola chiave "matrix" si può usare per definire esplicitamente
la matrice di trasformatione per oggetti ou testura (texture).
La sintassi generale di questa parola chiave:
matrix <m00, m01, m02,
m10, m11, m12,
m20, m21, m22,
m30, m31, m32> |
Qui i valori numerici mij
possono essere di tutti i tipi d'espressioni per numeri reali.
Formano gli elementi delle 3 prime colonne di una 4x4 matrice con la quarta colonna
definito fisso con <0,0,0,1> .
Un punto P1(x1/y1/z1)
si trasforma in un punto altro P2(x2/y2/z2)
, con la definition seguente:
x2
= m00*x1
+ m10*y1
+ m20*z1
+ m30
y2 = m01*x1
+ m11*y1
+ m21*z1
+ m31
z2 = m02*x1
+ m12*y1
+ m22*z1
+ m32
|
Un poco troppo astratto - vero?
Qui qualche esempio per chiarire la situazione:
1) La matrice della corrispondenza identica:
matrix < 1, 0, 0,
0, 1, 0,
0, 0, 1,
0, 0, 0 > |
|
2) Questa matrice causa una traslazione (spostamento m parallelo)
con il vettore <2,3,4>:
matrix < 1, 0, 0,
0, 1, 0,
0, 0, 1,
2, 3, 4 > |
Lo stesso si può avere con il commando seguente (più effettivo e meglio da capire!):
translate< 2, 3, 4>. |
3) Rotation intorno alla asse y con un angelo di Alpha (misurato in gradi)
è causata dalla matrice seguente:
(Nota: seno e coseno in POV-Ray impóngono i valorie dei angoli in radiante!)
#declare A = radians(Alpha);
matrix<cos(A), 0, sin(A),
0 , 1, 0 ,
-sin(A), 0, cos(A),
0 , 0, 0 > |
Rotation intorno alla asse y con 30°
(sin30° = 0.5; cos30° = 0.886):
matrix <0.886, 0, 0.5,
0 , 1, 0,
-0.5 , 0, 0.886,
0 , 0, 0 > |
Lo stesso si può avere con il commando seguente (più effettivo e meglio da capire!):
rotate< 0, Alpha, 0> .
|
4) La matrice seguente causa un'espansione addizionale con il fattore k = 3
con il centero O(0/0/0):
matrix < 3, 0, 0,
0, 3, 0,
0, 0, 3,
0, 0, 0 > |
Anche questa orrispondenza si può avere più effettivo e meglio da capire con:
"scale<3,3,3>"
ou più facile con "scale 3" .
|
Questi esempii hanno dimonstrato come tutte le trasformazioni semplici possono
essere descritto con "matrix".
Normalmente
non usiamo matrici di trasformazione per tutte queste trasformazioni
(traslazione, cambiare scala, espansione centrico, rotazione),
perchè sono difficili da capire in questa forma.
Ma qui esiste un aspetto molto interessante nel commando "matrix":
Esistono corrispondenze affini di maniera più generale que non si può avere
in un modo altro, cioè lo scorrimento elastico (shearing).
La matrice seguente causa uno scorrimento elastico
di un oggetto ou di una testure in direzione del'asse y:
matrix < 1, 1, 0,
0, 1, 0,
0, 0, 1,
0, 0, 0 > |
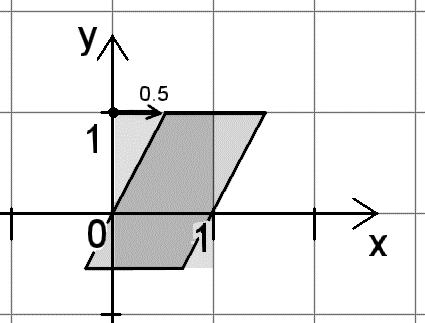
Uno scorrimento elastico in direzione y con 30°: |
matrix< 1 , 0, 0,
0.5, 1, 0,
0 , 0, 1,
0 , 0, 0 > |
|
|
La combinazione di corrispondenze differenti con matrici
spesso non sono facile da capire.
La matrice seguente può dimostrale.
Questa mactice ruota un oggetto intorno al asse y con 30° e poi causa uno scorramento elastico
in direzione y e una traslazione in direzione y:
matrix< 0.886, 0.5, 0.5 ,
0 , 1 , 0 ,
0 , 0 , 0.886,
0 , 1.5, 0 > |
Quest'esempio mostra perche è ricommandato di dividere corrispondenze di questo tipo
e farle passo a passo - se non abbiamo esperienza abbastanza con questo:
rotate<0,30,0>
//Shearing in y direction:
matrix<1, 0.5, 0,
0, 1 , 0,
0, 0 , 1,
0, 0 , 0 >
translate<0,1.5,0> |
Questi commandi fanno lo stesso!
|


