Trasformazioni Geometriche con POV-Ray - trasformzioni per vettori

Vettori e Trasformazioni
Trasformazioni per vettori et altre cose con vettori in POV-Ray:

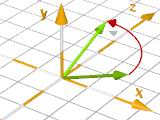
vrotate( V, <Rotate.x, Rotate.y, Rotate.z>)
Rotazione di un vettore V intorni al centro <0,0,0>
con un vettore di rotazione <Rotate_X, Rotate_Y, Rotate_Z>.

vrotate( < 2.5, 1, 0>,
          < 0, 90, 0> )

vaxis_rotate( V1, V2, A)
Rotazione del vettore V1 intorno al vettore V2 con A gradi
Rotazione di un vettore intorn un altro vettore come asse di rotazione.

vaxis_rotate(< 0, 1, 0.5>,
             < 2, 3,   0>,
                       70 )

vtransform ( V, Transformation )
vinv_transform( V , Transformation )
Bisogni: #include "transform.inc"
Combinare trasformazioni come translate, scale, rotate e matrix.
vtransform() applica una trasformazione di un punto.
vinv_transform() fa la trasformazione inversa ('undo').

#declare A = < 1.5, 0.3, 0.25 >;
#declare Trans1 =
   transform{ rotate<0,-50,0>
              translate<0,0.7,0> };
#declare B = vtransform ( A, Trans1 );

vturbulence(Lambda, Omega, Octaves, V)
Rende il vettore di turbolenza per il punto V sulla base dei valori indicati turbolenza. (Per Lambda, Omega, Octaves: POV-Ray Wiki.
L'ampiezza di turbolenza può essere controllata moltiplicando il vettore turbolenza. La frequenza a cui il vettore de la turbolenza si modifiche può essere controllato moltiplicando V.
Possiamo ottenere una versione turbulated del vettore V con :

#declare V_Turb =
    V + Ampl*vturbulence(2, 0.5, 6, V*Freq);

Example vturbulence.txt

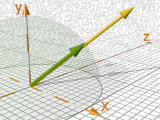
vnormalize( V )
Il vettore A normalizzato, un vettore della lunghezza di una unità nella direzione di A.
Formula: vnormalize(A)= A / vlength(A).
Attenzione:Utilizzando vnormalize(<0,0,0>) si tradurrà in un errore.

#if( vlength(V) != 0 )// if is not <0,0,0>
  #declare Vo = vnormalize( V );
#end

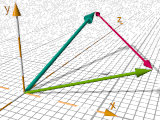
vcross( V1, V2)
Prodotto vettoriale di A e B (' A x B '),
Un vettore perpendicolare ai due vettori originali e con la lunghezza uguale alla superficie del parallelogramma definito da loro. Formula:
AxB = |A|*|B|*sin(angle(A,B))*perpendicular_unit_vector(A,B)
La lunghezza del vettore di prodotto vettoriale è proporzionale al seno dell'angolo tra A e B.

#declare YellowVector =
            vcross( BlueVextor, GreenVector);

vdot( V1, V2)
Prodotto scalare di V1 e V2. ('dot product', 'scalar product'). È direttamente proporzionale alla lunghezza dei vettori V1 e V2 e il coseno dell'angolo tra V1 e V2.
Se VDOT (A, B) = 0, allora VAngleD (A, B) = 90 gradi.
Formula: vdot=V1.x*V2.x + V1.y*V2.y + V1.z*V2.z.

#declare Vyellow =
 Vright*vdot(Vleft,Vright)/vdot(Vright,Vright);

vlength( V )
La lunghezza di V come un valore float.
Formula: length=sqrt(vdot(A,A)).

#declare Distance_AB = vlength( B-A );

VAngle( V1, V2 )
VAngleD( V1, V2 )
Bisogni: #include "math.inc"
Questi ritorno l'angolo tra il vettore V1 e V2.
Vangle() ritorno con l'angolo in radianti, VAngleD() in gradi.

VProject_Axis(V, Axis)
Bisogni: #include "math.inc"
Proiezione di un vettore V sul un asse Axis.
Formula: Axis*vdot(V, Axis)/vdot(Axis, Axis).

#declare YellowV =
      VProject_Axis( BlueV, GreenV);

Per queste trasformazioni si può usare dei modelli di testo della sezione "Shearing & transform" del mio "Insert Menu Add-on".

Descrizioni ed esempi per POV-Ray di Friedrich A. Lohmüller

Trasformazioni Geometriche con POV-Ray -

translate | rotate | scale | matrix | scorrimento elastico | transforms.inc | transform | trasformazioni di vettori

Descrizioni ed esempi per POV-Ray di Friedrich A. Lohmüller Trasformazioni Geometriche con POV-Ray -

translate | rotate | scale | matrix | scorrimento elastico | transforms.inc | transform | trasformazioni di vettori

Descrizioni ed esempi per POV-Ray di Friedrich A. Lohmüller

Trasformazioni Geometriche con POV-Ray -