matrix < , , >
Matrice et Carte Affine
Le mot clé "matrix"- peut être utilisé pour définir
explicitement la matrice de transformation des objet ou textures.
La syntaxe de celui-ci :
matrix <m00, m01, m02,
m10, m11, m12,
m20, m21, m22,
m30, m31, m32> |
Le nombre mij
peut être n'importe quelle sorte d'expressions numériques
Il forme les éléments des 3 premières colonnes d'une matrice 4x4,
dont la 4ème colonne est définie fixe en <0,0,0,1>.
Un point P1(x1/y1/z1)
est inplémenté dans un autre point P2(x2/y2/z2)
, selon la définition suivante :
x2
= m00*x1
+ m10*y1
+ m20*z1
+ m30
y2 = m01*x1
+ m11*y1
+ m21*z1
+ m31
z2 = m02*x1
+ m12*y1
+ m22*z1
+ m32
|
Un peu abstrait, n'est-ce pas ?
Voici quelques exemples pour le clarifier :
1) La matrice identité :
matrix < 1, 0, 0,
0, 1, 0,
0, 0, 1,
0, 0, 0 > |
|
2) Cette matrice produit une translation parallèle par le vecteur <2,3,4>:
matrix < 1, 0, 0,
0, 1, 0,
0, 0, 1,
2, 3, 4 > |
La même, mais plus efficace et plus facile à comprendre :
translate< 2, 3, 4>. |
3) Rotation autour d'un axe avec un angle Alpha
(mesuré en degrés) produite par la matrice suivante :
(Remarque : sinus et cosinux en POV-Ray ont besoin de leurs arguments
quand l'angle est en radians !)
#declare A = radians(Alpha);
matrix<cos(A), 0, sin(A),
0 , 1, 0 ,
-sin(A), 0, cos(A),
0 , 0, 0 > |
Rotation autour de »y« de 30°
(sin30° = 0.5; cos30° = 0.886):
matrix <0.886, 0, 0.5,
0 , 1, 0,
-0.5 , 0, 0.886,
0 , 0, 0 > |
Même chose, seulement plus efficace
et se comprenant mieux, est décrite par la commande :
rotate< 0, Alpha, 0> .
|
4) La matrice suivante produit un étirement d'un
facteur de k = 3 avec le centre en O(0/0/0):
matrix < 3, 0, 0,
0, 3, 0,
0, 0, 3,
0, 0, 0 > |
Cette description peut être définie par "scale<3,3,3>"
ou plus simplement par "scale 3" plus facile et qui se comprend mieux.
|
Ces exemples ont montré que des transformations simples sont décrites avec
"matrix".
Normalement on n'utilise pas des matrices pour les transformations simples
(translation, scaling = centric streching, rotation), parce-que c'est difficile
à comprendre et demande beaucoup d'effort.
Mais il existe un aspect intérêssant de l'instruction »matrix« :
Celle-ci permet aussi de définir précisement le type général que l'on
ne peut obtenir d'une autre façon tel que
par exemple le crénellage »shearing«.
Cette matrice produit un crénellage ou une texture selon l'axe »y« :
matrix < 1, 1, 0,
0, 1, 0,
0, 0, 1,
0, 0, 0 > |
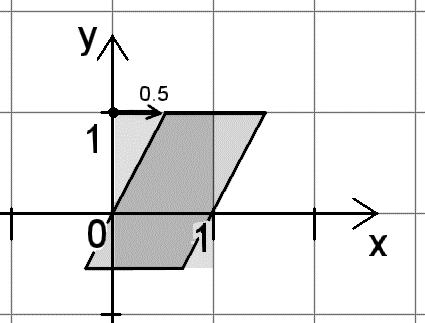
Un crénellage selon la direction »y«
avec facteur 0,5 (30°) est produit par : |
matrix< 1 , 0, 0,
0.5, 1, 0,
0 , 0, 1,
0 , 0, 0 > |
|
|
La combinaison de différentes cartes de matrices n'est pas facile à comprendre.
La matrice suivante peut le montrer. Cette-ci effectue une rotation d'un objet
autour de â??yâ?? de 30 degrés ensuite c'est crénellé selon »y« et une
translation parallèle dans la direction »y« :
matrix< 0.886, 0.5, 0.5 ,
0 , 1 , 0 ,
0 , 0 , 0.886,
0 , 1.5, 0 > |
Cela montre ce qui est recommandé » si vous n'avez pas
beaucoup d'expérience avec le mapping « la façon de
diviser de tels mappings en le faisant étape par étape:
rotate<0,30,0>
//Shearing in y direction:
matrix<1, 0.5, 0,
0, 1 , 0,
0, 0 , 1,
0, 0 , 0 >
translate<0,1.5,0> |
Cette instruction fait pareil !
|


