Beschreibungen und Beispiele zum Raytracer POV-Ray von Friedrich A. Lohmüller
Geometrische Transformationen in POV-Ray
English English English
Italiano Italiano
Français français
Home
- POV-Ray Tutorial
  Geometrische
  Transformationen
   - Inhalt

    Elementare
    Transformationen
    - "translate<  ... >"
    - "rotate<  ... >"
    - "scale<  ... >"
    - Spiegelung

    Weitere
    Transformationen
    - "matrix<  ... >"
    - Scherung
    - transforms.inc

    - "transform {  ...  } "
       und "inverse"

    Vektoren und
    Transformationen

    Insert Menu Zusatz
    & Download
 
                                           
Normal senkrecht Scherung

matrix < , , >
Matrizen und affine Abbildungen

Das "matrix"-Schlüsselwort kann dazu benutzt werden
explizit die Transformationsmatrix für Objekte oder Texturen festzulegen.
Der Syntax des Schlüsselwortes: 
 matrix <m00, m01, m02,
         m10, m11, m12,
         m20, m21, m22,
         m30, m31, m32>

wobei die Zahlen mij beliebige Kommazahlen- Ausdrücke ("float expressions")
sein dürfen, welche die Elemente der ersten 3 Spalten einer 4x4-Martrix darstellen, deren 4. Spalte hierbei fest als <0,0,0,1> definiert ist.
Ein Punkt P1(x1/y1/z1) wird in einen Punkt P2(x2/y2/z2) transformiert, wobei gilt:

x2 = m00*x1 + m10*y1 + m20*z1 + m30
y2 = m01*x1 + m11*y1 + m21*z1 + m31
z2 = m02*x1 + m12*y1 + m22*z1 + m32
Hier einige Beispiele:

1) Matrix der identischen Abbildung:
matrix < 1, 0, 0,
         0, 1, 0,
         0, 0, 1,
         0, 0, 0 >
2) Diese Matrix bewirkt eine Parallel-Verschiebung um den Vektor <2,3,4>:
matrix < 1, 0, 0,
         0, 1, 0,
         0, 0, 1,
         2, 3, 4 >
   Dasselbe, nur wesentlich rationeller u. anschaulicher, beschreibt der Befehl:    translate< 2, 3, 4>.
3) Drehung um die y-Achse mit einen Winkel Alpha (in Grad) durch die folgende Matrix:
(Besonderheit: sin und cos benötigen in POV-Ray das Winkel-Argument in Radians!)
 
#declare A = radians(Alpha);
matrix<cos(A), 0, sin(A),
          0  , 1,    0  ,
      -sin(A), 0, cos(A),
          0  , 0,    0   >

Drehung um die y-Achse um 30°
(sin30° = 0.5; cos30° = 0.886): 

matrix <0.886, 0,   0.5,
          0  , 1,     0,
       -0.5  , 0, 0.886,
          0  , 0,     0 >

Dasselbe, nur ebenfalls rationeller und anschaulicher, beschreibt der bekannte Befehl: rotate< 0, ß, 0> .

 4) Die folgende Matrix bewirkt eine zentrische Streckung um den Streckungsfaktor k = 3 mit dem Ursprung O(0/0/0) als Zentrum: 
matrix < 3, 0, 0,
         0, 3, 0,
         0, 0, 3,
         0, 0, 0 >

Auch diese Abbildung ist mittels "scale< 3, 3, 3>" oder einfacher durch "scale 3" leichter und anschaulicher zu erreichen.

Diese Beispiele zeigen, daß sich mit "matrix" alle einfachen Abbildung erreichen lassen. Für gewöhnlich wird man für einfachere Transformationen (Verschiebung, Skalierung = zentrische Streckung, Drehung) keine Transformationsmatrix verwenden, da sie die Abbildung mit größerem Aufwand beschreibt und schwerer vorzustellen ist. Es gibt jedoch einen interessanten Aspekt des Matrizenbefehls: Er erlaubt allgemeinere affine Abbildungen, wie z.B. die Scherung (shering), welche auf andere Weise nicht zu erreichen sind.

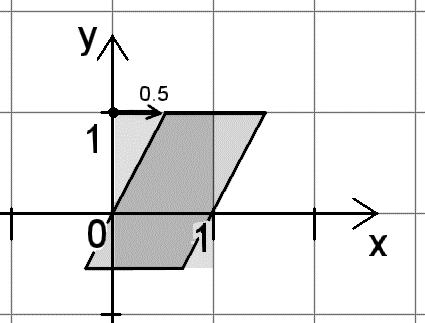
Eine Scherung längs der x-Richtung um 30°
mit der z-Achse als Fixgerade bewirkt:


  matrix< 1 , 0, 0,
         0.5, 1, 0,
          0 , 0, 1,
          0 , 0, 0 >


Hintereinander-Ausfühung verschiedener Abbildungen sind bei Matrizen selten optisch leicht zu trennen. Die folgende Matrix mag dies verdeutlichen. Sie rotiert um die y-Achse um 30° und schert längs der y-Achse und verschiebt parallel in y-Richtung:

 matrix< 0.886, 0.5,  0.5  ,
           0  , 1  ,  0    ,
           0  , 0  ,  0.886,
           0  , 1.5,  0     >


Es ist daher empfehlenswert solche wenig durch- schaubare Abbildungsanhäufungen, sofern man wenig Routine besitzt, möglichst klassisch, d.h. getrennt abzuhandeln:

rotate<0,30,0>
//Scherung in y-Richtung:
 matrix<1, 0.5, 0,
        0, 1  , 0,
        0, 0  , 1,
        0, 0  , 0 >
 translate<0,1.5,0>

Diese Befehlsfolge bewirkt dasselbe.

Streckungen mit Linearer Algebra

Die folgenden Abbildungen in Raum lassen sich mittels Abbildungsmatrizen in Form von einfachen 3x3-Matrizen mathematisch beschreiben. Dabei sind ausschließlich die Diagonalelemente ungleich Null.
Diese lassen sich in POVRAY sowohl mit dem Kommando "matrix<...>" als auch mit dem einfacheren Befehl "scale< ...>" realisieren.
Zentrische Streckung bzgl. Ursprung(0/0/0)
(gleicher Faktor k in alle Richtungen)
Abbildungsmatrix A = 
 matrix <k, 0, 0,
         0, k, 0,
         0, 0, k,
         0, 0, 0 >
   
kurz: "scale k " oder "scale<k,k,k>"

Parallel-Streckung
(nur in eine Richtung bzgl. Koordinatenebene, sonst konstant),
Abbildungsmatrix A = 
 matrix <k, 0, 0,
         0, 1, 0,
         0, 0, 1,
         0, 0, 0 >
    
kurz: "scale<k,1,1>"

Euler-Affinität
(in jede Richtung bzgl. Koordinatenebenen mit anderem Faktor)
Abbildungsmatrix A = 
 matrix <p, 0, 0,
         0, q, 0,
         0, 0, r,
         0, 0, 0 >
    
kurz: "scale<p,q,r>"
Weiterführende Literatur:
"Mathematik Sekundarstufe II - Analytische Geometrie und lineare Algebra - Erweiterte Ausgabe "
diverse Verfasser, Cornelsen Verlag, Berlin, 1993, ISBN 3-590-12319-2
(Befaßt sich leider nur mit 2dimensionalen affinen Abbildungen)

Hinweis:
"matrix" kann sowohl auf Körper, als auch auf andere Objekte wie Texturen("texture"), Farbmuster ("pigment"), scheinbare Oberflächenverformungen ("normal") angewandt werden.

translate | rotate | scale | matrix | Scherung | transforms.inc | transform | Vektor-Transformationen
top
© Friedrich A. Lohmüller, 2008
www.f-lohmueller.de