Home
- POV-Ray Tutorial
Geometric
Transformations
- Index
Elementary
Transformations
- "translate< ... >"
- "rotate< ... >"
- "scale< ... >"
- mirror symmetry
Other
Transformations
- "matrix< ... >"
- Shearing
- transforms.inc
- "transform{ ...}"
and "inverse"
Vectors and
Transformations
- vrotate
- vaxis_rotate
- vtransform
- vinv_transform
- vturbulence
- vnormalize
- vcross
- vdot()
- vlength()
- VAngle(), VAngleD()
- VProject_Axis
Insert Menu Add-on
& Download
|
|
Vectors and Transformations
Vector transformations and other vector related things in POV-Ray:
|
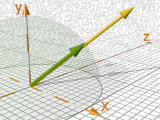
vrotate( V, <Rotate.x, Rotate.y, Rotate.z>)
Rotation of a vector V around the center <0,0,0>
by a rotation vector <Rotate.x, Rotate.y, Rotate.z>.
vrotate( < 2.5, 1, 0>,
< 0, 90, 0> ) |
|
|
|
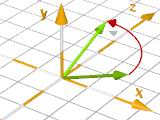
vaxis_rotate( V1, V2, A)
Rotates a vector V1 around a vector V2 as axis of rotation by A degrees.
vaxis_rotate(< 0, 1, 0.5>,
< 2, 3, 0>,
70 ) |
|
|
|
vtransform ( V, Transformation )
vinv_transform( V , Transformation )
Needs: #include "transform.inc"
Combining transformations translate, scale, rotate and matrix.
vtransform() applies a transformation to a point.
vinv_transform() does the inverse transformation ('undo').
#declare A = < 1.5, 0.3, 0.25 >;
#declare Trans1 =
transform{ rotate<0,-50,0>
translate<0,0.7,0> };
#declare B = vtransform ( A, Trans1 ); |
|
|
|
vturbulence(Lambda, Omega, Octaves, V)
Returns the turbulence vector for the point V based on the given turbulence values.
(For Lambda, Omega, Octaves see POV-Ray Wiki.
The amplitude Ampl of turbulence can be controlled by multiplying the turbulence vector.
The frequency Freq at which the turbulence vector changes can be controlled by multiplying V.
We can get a turbulated version of the vector V by :
#declare V_Turb =
V + Ampl*vturbulence(2, 0.5, 6, V*Freq); |
|
Example vturbulence.txt
|
|
vnormalize( V )
Normalized vector A, a unit length vector in direction of A.
Formula: vnormalize(A)= A / vlength(A).
Warning: Using vnormalize(<0,0,0>) will result in an error.
#if( vlength(V) != 0 )// if is not <0,0,0>
#declare Vo = vnormalize( V );
#end |
|
|
|
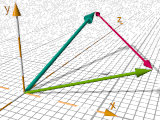
vcross( V1, V2)
Cross product of A and B (' A x B '),
A vector perpendicular to the two original vectors and
with the length equal to the area of the parallelogram defined by them. Formula:
AxB = |A|*|B|*sin(angle(A,B))*perpendicular_unit_vector(A,B)
The length of the cross product vector is proportional to the sine of the angle between A and B.
#declare YellowVector =
vcross( BlueVextor, GreenVector); |
|
|
|
vdot( V1, V2)
Dot product of V1 and V2. ('scalar product').
It's directly proportional to the length of the vectors V1 and V2
and the cosine of the angle between V1 and V2.
If vdot(A,B) = 0, then VAngleD(A,B) = 90 degrees.
Formula: vdot=V1.x*V2.x + V1.y*V2.y + V1.z*V2.z.
#declare Vyellow =
Vright*vdot(Vleft,Vright)/vdot(Vright,Vright); |
|
|
|
vlength( V )
Returns the length of V as a float value.
Formula: vlength=sqrt(vdot(A,A)).
#declare Distance_AB = vlength( B-A ); |
|
|
|
VAngle( V1, V2 )
VAngleD( V1, V2 )
Needs: #include "math.inc"
These return the angle between the vectors V1 and V2.
VAngle() returns the angle in radians, VAngleD() in degrees.
|
|
|
VProject_Axis(V, Axis)
Needs: #include "math.inc"
Projects a vector V onto the an axis Axis.
Formula: Axis*vdot(V, Axis)/vdot(Axis, Axis).
#declare YellowV =
VProject_Axis( BlueV, GreenV); |
|
|
The vector transformations shown here are also available as text templates
in the section "Shearing & transform"
in my "Insert Menu Add-on"
.
|