Transformations géométriques avec POV-Ray - Transformations de vecteurs

Vecteurs et Transformations
Des transformations des vecteurs et autres choses avec vecteurs en POV-Ray:

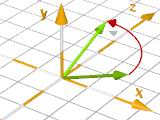
vrotate( V, <Rotate.x, Rotate.y, Rotate.z>)
Rotation d'un vecteur V autour du center <0,0,0>
par un vecteur de rotation <Rotate_X, Rotate_Y, Rotate_Z>.

vrotate( < 2.5, 1, 0>,
          < 0, 90, 0> )

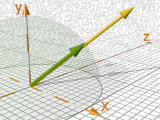
vaxis_rotate( V1, V2, A)
Rotation de V1 autour de V2 par A degrés.
Rotation d'un vecteur autour un autre vecteur comme l'axe de rotation.

vaxis_rotate(< 0, 1, 0.5>,
             < 2, 3,   0>,
                       70 )

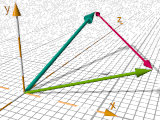
vtransform ( V, Transformation )
vinv_transform( V , Transformation )
Il exige : #include "transform.inc"
Combination de transformations comme translate, scale, rotate et matrix.
vtransform() applique une transformation à un point.
vinv_transform() fait la transformation inverse ('undo').

#declare A = < 1.5, 0.3, 0.25 >;
#declare Trans1 =
   transform{ rotate<0,-50,0>
              translate<0,0.7,0> };
#declare B = vtransform ( A, Trans1 );

vturbulence(Lambda, Omega, Octaves, V)
Retour avec le vecteur de turbulence pour le point V sur la base des valeurs de turbulence proposés. (Lambda, Omega, Octaves : POV-Ray Wiki.
L'amplitude Ampl de la turbulence peut être contrôlée an multipliant le vecteur de la turbulence. La frequency Freq la fréquence à laquelle les changements de vecteur de turbulence peuvent être contrôlée en multipliant V.
Nous pouvons obtenir une version du vecteur V avec turbulence par :

#declare V_Turb =
    V + Ampl*vturbulence(2, 0.5, 6, V*Freq);

Example vturbulence.txt

vnormalize( V )
Un vecteur normalisé, un vecteur d'unité de longueur dans la direction de A.
Formule : vnormalize(A)= A / vlength(A).
avertissement:
Utiliser vnormalize (<0,0,0>) entraînera une erreur.

#if( vlength(V) != 0 )// if is not <0,0,0>
  #declare Vo = vnormalize( V );
#end

vcross( V1, V2)
Le produit vectoriel de A et B (' A x B '),
un vecteur perpendiculaire aux deux vecteurs d'origine et avec la longueur égale à la surface du parallélogramme défini par eux. Formule:
AxB = |A|*|B|*sin(angle(A,B))*perpendicular_unit_vector(A,B)
La longueur du vecteur du produit vectoriel est proportionnel au sinus de l'angle entre A et B.

#declare YellowVector =
            vcross( BlueVextor, GreenVector);

vdot( V1, V2)
Produit scalaire de V1 et V2. ('dot product', 'scalar product'). Il est directement proportionnel à la longueur des vecteurs V1 et V2 et le cosinus de l'angle entre V1 et V2.
Si Vdot (A, B) = 0, alors VAngleD (A, B) = 90 degrés.
Formule : vdot=V1.x*V2.x + V1.y*V2.y + V1.z*V2.z.

#declare Vyellow =
 Vright*vdot(Vleft,Vright)/vdot(Vright,Vright);

vlength( V )
Retourne la longueur de V comme un nombre à virgule.
Formule : vlength = sqrt(vdot(A,A)).

#declare Distance_AB = vlength( B-A );

VAngle( V1, V2 )
VAngleD( V1, V2 )
Il exige : #include "math.inc"
Ce retour de l'angle entre les vecteurs V1 et V2.
VAngle() renvoie l'angle en radians, VAngleD() en degrés.

VProject_Axis(V, Axis)
Il exige : #include "math.inc"
La projection d'un vecteur V sur l'd'un axe Axis.
Formule : Axis*vdot(V, Axis)/vdot(Axis, Axis).

#declare YellowV =
      VProject_Axis( BlueV, GreenV);

Pour les transformations représentées ici on peut utiliser mes modèles de texte de la section "Shearing & transform" en mon "Insert Menu Add-on" .

Descriptions et exemples pour le POV-Ray raytracer par Friedrich A. Lohmüller

Transformations géométriques avec POV-Ray -

translate | rotate | scale | matrix | cisaillement | transforms.inc | transform | transformations de vecteurs

Descriptions et exemples pour le POV-Ray raytracer par Friedrich A. Lohmüller Transformations géométriques avec POV-Ray -

translate | rotate | scale | matrix | cisaillement | transforms.inc | transform | transformations de vecteurs

Descriptions et exemples pour le POV-Ray raytracer par Friedrich A. Lohmüller

Transformations géométriques avec POV-Ray -