Home
- POV-Ray Tutorial
Geometrische
Transformationen
- Inhalt
Elementare
Transformationen
- "translate< ... > "
- "rotate< ... > "
- "scale< ... > "
- Spiegelung
Weitere
Transformationen
- "matrix< ... >"
- Scherung
- transforms.inc
- "transform { ... }"
und "inverse"
Vektoren und
Transformationen
- vrotate
- vaxis_rotate
- vtransform
- vinv_transform
- vturbulence
- vnormalize
- vcross
- vdot()
- vlength()
- VAngle(), VAngleD()
- VProject_Axis
Insert Menu Zusatz
& Download
|
|
Vektoren und Transformationen
Vektortransformationen und andere vektorbezogene Makros in POV-Ray:
|
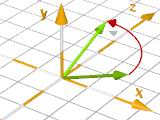
vrotate( V, <Rotate.x, Rotate.y, Rotate.z>)
Rotation eines Vektors V um den Ursprung <0,0,0>
mit dem Rotationsvektor <Rotate_X, Rotate_Y, Rotate_Z>.
vrotate( < 2.5, 1, 0>,
< 0, 90, 0> ) |
|
|
|
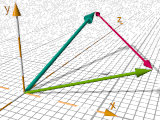
vaxis_rotate( V1, V2, A)
Rotatiert V1 um V2 um A Grad
Rotation eines Vektors um einen anderen Vektor als Drehachse.
vaxis_rotate(< 0, 1, 0.5>,
< 2, 3, 0>,
70 ) |
|
|
|
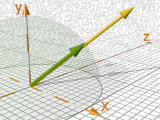
vtransform ( V, Transformation )
vinv_transform( V , Transformation )
Benotigt: #include "transform.inc"
Kombiniert Transformationen 'translate', 'scale', 'rotate' und 'matrix'.
vtransform() wendet eine Transformation auf einen Punkt an.
vinv_transform() macht die inverse Transformation ('undo').
#declare A = < 1.5, 0.3, 0.25 >;
#declare Trans1 =
transform{ rotate<0,-50,0>
translate<0,0.7,0> };
#declare B = vtransform ( A, Trans1 ); |
|
|
|
vturbulence(Lambda, Omega, Octaves, V)
Erzeugt den Turbulenz-Vektor für den Punkt V basierend auf den gegebenen Turbulenz-Werten.
(Für Lambda, Omega, Octaves siehe POV-Ray Wiki.
Die Amplitude Ampl der Turbulence kann durch Multiplizieren des Turbulenz-Vektors gesteuert werden.
Die Frequenz Freq mit der sich die Turbulenz ändert kann durch Multiplizieren von V gesteuert werden.
Wir erhalten eine turbulierte Version des Vektors V durch:
#declare V_Turb =
V + Ampl*vturbulence(2, 0.5, 6, V*Freq); |
|
Beispiel vturbulence.txt
|
|
vnormalize( V )
Normierter Vektor A, ein Einheitsvektore in Richtung von A.
Formel: vnormalize(A)= A / vlength(A).
Warnung: Die Verwendung von vnormalize(<0,0,0>) erzeugt einen Error!
#if( vlength(V) != 0 )// if is not <0,0,0>
#declare Vo = vnormalize( V );
#end |
|
|
|
vcross( V1, V2)
Kreuz-Produkt oder Vektorprodukt von A und B (' A x B '),
ein Vektor senkrecht zu den beiden orginalen Vektoren und
mit einer Länge, die dem Flächeninhalt des Parallelogramms aus A und B. Formel:
AxB = |A|*|B|*sin(angle(A,B))*senkrechter_Einheitsvektor(A,B)
Die Länge des Krezprodukt-Vektors ist proportional zum Sinus des Winkels zwischen A und B.
#declare YellowVector =
vcross( BlueVextor, GreenVector); |
|
|
|
vdot( V1, V2)
Skalarprodukt von V1 und V2. ('dot product', 'scalar product').
Dies ist direkt proportional zur den Längen der Vektoren V1 und V2
und dem Kosinus des Winkels zwischen V1 und V2.
Wenn vdot(A,B) = 0, dann VAngleD(A,B) = 90 Grad.
Formel: vdot=V1.x*V2.x + V1.y*V2.y + V1.z*V2.z.
#declare Vyellow =
Vright*vdot(Vleft,Vright)/vdot(Vright,Vright); |
|
|
|
vlength( V )
Ergibt die Länge von V als eine Kommazahl.
Formel: vlength=sqrt(vdot(A,A)).
#declare Distance_AB = vlength( B-A ); |
|
|
|
VAngle( V1, V2 )
VAngleD( V1, V2 )
Benötoigt: #include "math.inc"
Dies ergibt den Wert des Winkels zwischen den Vektoren V1 und V2.
VAngle() ergibt den Winkel in Radiant, VAngleD() in Grad.
|
|
|
VProject_Axis(V, Axis)
Benötigt: #include "math.inc"
Projektion eines Vektors V auf eine Achse 'Axis'.
Formel: Axis*vdot(V, Axis)/vdot(Axis, Axis).
#declare YellowV =
VProject_Axis( BlueV, GreenV); |
|
|
Die hier dargestellten Vektor-Transformationen können im Abschnitt "Shearing & transform"
in meinem "Insert Menu Add-on"
als Text-Schablonen verwendet werden.
|