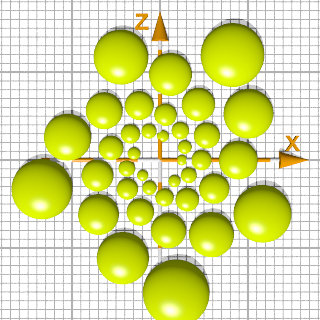
#local R = 0.25; // start radius
#local Nr = 0; // start
#local End_Nr = 37; // end
#while ( Nr <= End_Nr ) // loop
sphere{ <0,0,0>, R*0.25 //------------
scale <1,0.6,1>
texture{
pigment{color rgb<0.8,1,0>}
finish {phong 1}
} //--------------
translate <R,0,0>
rotate <0,-Nr*360*(8/13),0>
} //-----------------------------
#local R = R*1.05; // growing radius
#local Nr = Nr + 1; // next Nr
#end // --------------- end of loop |
Le même precedure avec une boucle for :
#local R = 0.25; // start radius
//#for(Identifier,Start,End[,Step])
#for ( Nr , 0, 37, 1 )
sphere{ <0,0,0>, R*0.25 //------------
scale <1,0.6,1>
texture{
pigment{color rgb<0.8,1,0>}
finish {phong 1}
} //--------------
translate <R,0,0>
rotate <0,-Nr*360*(8/13),0>
} //-----------------------------
#local R = R*1.05; // growing radius
#end // --------------- end of loop |
|
// Fibonacci numbers:
// Règles: A(1)= 1; A(2) = 1; and
// pour N>2: A(N) = A(N-1) + A(N-2).
// 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ...
|
|
Avec une augmentation linéaire du rayon R
nous obtenons la forme suivante :
#local R = 0.018; // start radius
#local Nr = 0; // start
#local End_Nr = 300; // end
#while ( Nr <= End_Nr ) // loop
sphere{ <0,0,0>,0.25 + Nr*0.0015 //----
scale <1,1.6,1>
texture{
pigment{color rgb<1,0.7,0>}
finish {phong 1}
} //--------------
translate <R*0.65,0,0>
rotate <0,-Nr*360*(34/89),0>
} //-----------------------------
#local R = R+0.038; // growing radius
#local Nr = Nr + 1; // next Nr
#end // --------------- end of loop |
|
|