Transformations géométriques avec POV-Ray

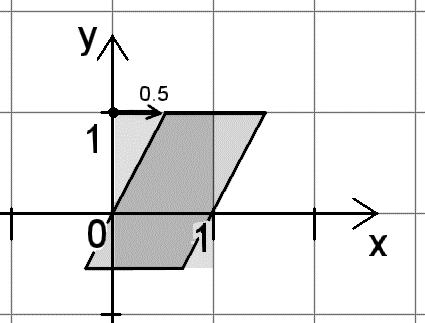
Cisaillement avec matrix < , , >

Il n'est pas recommandé de définir à l'aide de matrices des transformations simples comme les translations (translate), les changements d'échelles (scale) ou les rotations (rotate), car cela les rend très difficile à comprendre.
Le cisaillement est une transformation simple descriptible seulement avec une matrice "matrix" en POV-Ray.

Exemple : Cisaillement de l'axe y en direction x avec fakteur 0.5 (30°):


  matrix< 1 , 0, 0,
         0.5, 1, 0,
          0 , 0, 1,
          0 , 0, 0 >

Marices de cisaillement avec une représentation graphique des effets :

matrix < 1,0.5,  0,
         0,  1,  0,
         0,  0,  1,
         0,  0,  0 >

matrix < 1,  0,0.5,
         0,  1,  0,
         0,  0,  1,
         0,  0,  0 >

matrix < 1,  0,  0,
       0.5,  1,  0,
         0,  0,  1,
         0,  0,  0 >

matrix < 1,  0,  0,
         0,  1,0.5,
         0,  0,  1,
         0,  0,  0 >

matrix < 1,  0,  0,
         0,  1,  0,
       0.5,  0,  1,
         0,  0,  0 >

matrix < 1,  0,  0,
         0,  1,  0,
         0,0.5,  1,
         0,  0,  0 >

Pour les matrices de cisaillement représentées ici on peut utiliser mes modèles de texte de la section "Shearing & transform" en mon "Insert Menu Add-on".

Descriptions et exemples pour le POV-Ray raytracer par Friedrich A. Lohmüller

Transformations géométriques avec POV-Ray -

Cisaillement avec matrix < , , >

Exemple : Cisaillement de l'axe y en direction x avec fakteur 0.5 (30°):

Marices de cisaillement avec une représentation graphique des effets :

Pour les matrices de cisaillement représentées ici on peut utiliser mes modèles de texte de la section "Shearing & transform" en mon "Insert Menu Add-on".

translate | rotate | scale | matrix | cisaillement | transforms.inc | transform | transformations de vecteurs

Descriptions et exemples pour le POV-Ray raytracer par Friedrich A. Lohmüller Transformations géométriques avec POV-Ray -

Cisaillement avec matrix < , , >

Exemple : Cisaillement de l'axe y en direction x avec fakteur 0.5 (30°):

Marices de cisaillement avec une représentation graphique des effets :

Pour les matrices de cisaillement représentées ici on peut utiliser mes modèles de texte de la section "Shearing & transform" en mon "Insert Menu Add-on".

translate | rotate | scale | matrix | cisaillement | transforms.inc | transform | transformations de vecteurs

Descriptions et exemples pour le POV-Ray raytracer par Friedrich A. Lohmüller

Transformations géométriques avec POV-Ray -