Home
- POV-Ray Tutorials
POV-Ray Introduction
Content - INDEX
1. Working with POV-Ray:
"Insert Menu Add-on".
2. Basics on
How To Make a Scene.
3D Coordinates,
Floats and Vectors
3. Scene Structure
Basic example.
4. Scene File Header,
#include files,
camera, light_source.
>5. Basic Geometric Objects
sphere, box, cylinder,
cone, torus, plane.
and other shapes
6. Transformations
Streching, Turning,
Moving and others.
CSG: union,
difference, intersection.
7. Colors on Surfaces
texture, pigment, normal, finish
8. #declare, #local, #macro,
placeholders + flexible objects.
9. #while Loops
Basic examples.
10. #include, include files,
re-usable objects.
11. Efficiency,
speed, flexibility,
modulare working
adapting from 3.1 to 3.5;3.6
adapting from 3.5;3.6 to 3.7
POV-Ray + Windows Vista.
- Insert Menu Add-on
& Download
|
The Basic Geometric Objects:
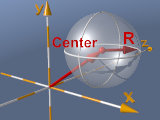
sphere - ball:
sphere{ <0,1,0>, 0.5
texture{ Polished_Chrome }
translate<0,1.35,0>
} |
Center <xM.yM,zM>, radius
|
|
|
|
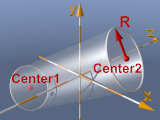
cylinder - tube:
cylinder{ <0,0,0>,<0,1,0>, 0.25
pigment{color rgb<1,0.6,0>}
} |
Center 1 <xM1,yM1,zM1>,
center 2 <xM2,yM2,zM2>, radius |
|
|
|
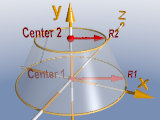
cone - trunced cone / conus:
cone{ <0,0,0>, 1, <0,1.75,0>, 0.5
pigment{color rgb<0.4,0.7,0>}
finish {phong 1}
} |
Center 1 <xM1,yM1,zM1>, radius 1,
center 2 <xM2,yM2,zM2>, radius 2. |
|
|
|
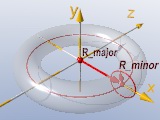
torus - ring / tire:
torus{ 1.00, 0.25
rotate<90,0,0>
translate<-0.5, 1+0.25, 0>
pigment{ color rgb<1,0.8,0>}
finish { phong 1}
} |
Radius from the ring center to the tire: rmajor,
and radius of the tire: ,rminor.
The torus shape is placed in the xz plane, his axis is the y axis.
With this sample you will get a ring that is standing vertical in the xy plane
with his axis parallel to the z axis. |
|
|
|
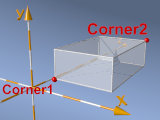
box - cuboid, rectangular parallelepiped:
box{ <0,0,0>, <1,2,4>
pigment{ checker
color rgb<1,1,1>
color rgb<1,1,1>*0
scale <0.5,0.25,0.5> }
} |
Two opposite corners: <x1.y1,z1>
<x2,y2,z2> :
A box from x1 to x2,
from y1 to y2 and
from z1 to z2.
|
|
|
|
prism - ortogonal prism:
prism{ 0.00, 1.00, 4,
<-1.00,0.00>, <1.00,0.00>, <0.00,-1.30>, <-1.00,0.00>
pigment{ color White }
} |
From y =... , to y = ..., number of points of the base,
xz coordinates separated by commas.
The prism is placed with it's parallel sides parallel to the y-axis and is defined by
the edges of it's sectional view, which is in it's basic form defined in the xz plane.
By rotations of 90° around an axis, it is possible to get prisms in z direction,
in x-direction or in any other directions! |
|
|
plane - infinite plane, more precise: a half space!
plane{ <0,1,0>, 0
texture{ Cork }
} |
<0,1,0> = "surface normal".
In < , , >, 0
the 4th float defines the distance to <0,0,0>!
The surface normal is a vector that stands vertical on the plane.
Here: < 0, 1, 0> points to positive direction of y,
that means the plane is horizontal, it is the xz plane.
Strictly speaking this "plane" defines a "half space", which contains the space behind
(or under) this plane, right opposite to where the "surface normal" is pointing to.
This is important, if you use the object "plane" in "union",
"difference" or "intersection" ( see: "CSG" ), because this "half space"
is the "inside" of the plane.
|
|
|
A great variety of other geometric objects
see here: Geometric Shapes in POV-Ray.
|
|
height_field
|
text object
|
isosurface
|
isosurface
|
polyhedra
|
parametric
|
|
|
| top |
© Friedrich A. Lohmüller, 2014
homepage:www.f-lohmueller.de
|