Home
- POV-Ray Tutorial
- Geometrical Basics
for Raytracing
Right-angled Triangle
Pythagorean Theorem
Trigonometry Basics
Law of cosines
Equilateral Triangle
Regular Polygon
Polyhedron
Tetrahedron
Octahedron
Cube & Cuboid
Dodecahedron
Icosahedron
Cuboctahedron
Truncated Octahedron
Rhombicuboctahedron
Truncated Icosahedron
Circles
Tangent Circles
Internal Tangents
External Tangents
- Geometric 3D Animations
|
External Tangents to two Circles
In the following we write for the square root of a number the expression "sqrt(NUMBER)" and "abs(NUMBER)" for |NUMBER|,
conforming to the syntax used in POV-Ray.
Note: Here objects in 2D geometry are represented by 3D shapes in the xy-plane.
Therefore all coordinates must have the z-components zero! ( <?,?,0>) |
|
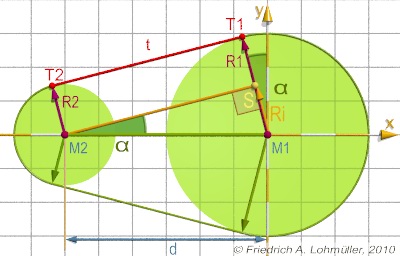
We want the external tangents to the tangent points
T1 and T2 of two circles C1(M1,r1) and C2(M2,r2) with
the radii r1 > r2 ,
as shown in the opposite image.
The distance of their centers is d.
The difference of their radii is ri = r1 - r2.
|
The triangle M1,S,M2 has a right angle at S.
The line(T1,T2) is parallel to the line(M2,S) and has the same length.
So t = |T1,T2| = sqrt( d2 - ri2).
The angle α = atan(ri/t). or α = asin(ri/d).
|
The calulation of the length of the belt around:
The length of the segment around the circle C1:
l1 = 2π·r1 ·(180+2·α)/360.
The length of the segment around the circle C2:
l2 = 2π·r2 ·(180-2·α)/360.
The length of the complete belt is:
l = l1 + l2 + 2·t .
|
|
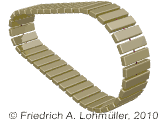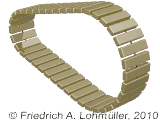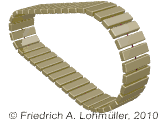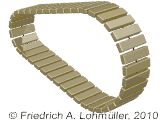
External tangents to two circles rendered with POV-Ray
|
|
For what can we use this geometry?
Here some examples:
|
|
|
A round conic torus.
|
A round conic prism.
|
|
|
|
|
|
| top
|
|