Home
- Tutorial POV-Ray
- Geometria di Base
per Raytracing
Triangolo Rettangolo
Teorema di Pitagora
Trigonometria di Base
Teorema del Coseno
Triangolo Equilatero
Poligono Regulare
Poliedro
Tetraedro Regolare
Ottaedro Regolare
Cubo e Cuboide
Dodecaedro Regolare
Icosaedro Regolare
Cubottaedro
Ottaedro troncato
Rombicubottaedro
Icosaedro troncato
Cerchi
Cerchi tangenti
Tangenti interne
Tangenti esterne
- Animazioni Geometriche 3D
|
Tangenti esterne
Nel seguente si scriva per la radice quadrata di un numero,
l'espressione inglese "sqrt(Numbero)"
in conformità alla sintassi usata con POV-Ray.
Nota: Qui oggetti in geometria 2D sono rapresentati con forme 3D nel piano di xy.
Per questo tutte le coordinate devono avere la componente di z zero! ( <?,?,0>) |
|
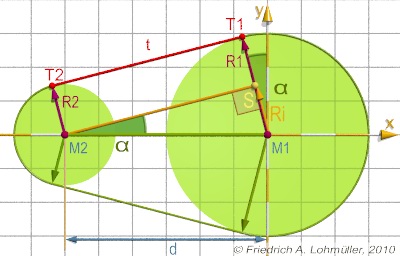
Cerchiamo una tangente esterna entro i punti di tangente
T1 e T2 di due cerchi C1(M1,r1)
e C2(M2,r2) con
i raggi r1 > r2 ,
come nella immagine a margine.
La distanza dei centri è d.
La differenza dei raggi è ri = r1 - r2.
|
Il triangolo M1,S,M2 ha un angolo retto al punto S.
La linea (T1,T2) è parallela a la linea(M2,S) e ha la stessa lunghezza.
Cosi t = |T1,T2| = sqrt( d2 - ri2).
L'angolo α = atan(ri/t). or α = asin(ri/d).
|
Il calcolo della lunghezza della cintura intorno:
La lunghezza del segmento intorno al cerchio C1:
l1 = 2π·r1 ·(180+2·α)/360.
La lunghezza del segmento intorno al cerchio C2:
l2 = 2π·r2 ·(180-2·α)/360.
La lunghezza della cintura completa è:
l = l1 + l2 + 2·t .
|
|
Tangente esterne di due cherchi con POV-Ray
|
|
Per che cosa si può usare questa geometria?
Qui qualche esempio:
|
|
|
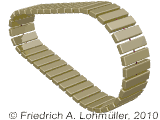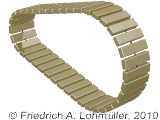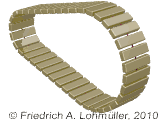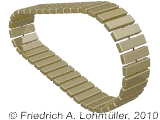
Un toro rotondo conico.
|
Un prisma rotondo conico.
|
|
|
|
|
|
| top
|
|