Page d'Accueil
- POV-Ray Tutorial
- Géométrie de Base
pour Raytracing
Triangle rectangle
Théorème de Pythagore
Trigonométrie de base
Loi des cosinus
Triangle équilatéral
Polygone régulier
Polyèdre
Tétraèdre régulier
Octaèdre régulier
Cube et Cuboïde
Dodécaèdre régulier
Icosaèdre régulier
Cuboctaèdre
Octaèdre tronqué
Rhombicuboctaèdre
Icosaèdre tronqué
Cercles
Cercles touchants
Tangentes internes
Tangentes externes
- Geometric 3D Animations
|
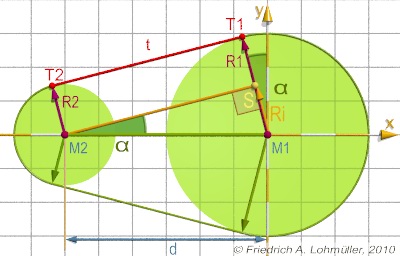
Tangentes externes aux deux Cercles
Note 1: En POV-Ray nous utilisons "sqrt(X)" pour la racine carrée de X
et nous utilisons "X*X" ou "pow(X,2)" pour X2.
Note 2: Les objets de la géométrie 2D sont représentés par des objets 3D dans le plan des xy.
Pour cela dans toutes les coordonnées herefore all coordinates le z-composant doit être zéro! ( <?,?,0> !) |
|
Nous cherchons les tangentes externes entre les points de tangente
T1 et T2 aux les deux cercles
C1(M1,r1) et C2(M2,r2)
avec les rayons r1 > r2,
comme figuré sur l'image ci-contre.
La distance des centres est d.
La différence des rayons est ri = r1 - r2.
|
Le triangle M1,S,M2 a un angle rectangle à S.
La ligne (T1,T2) est parallèle à la ligne (M2,S) et a la même longueur.
Ansi t = |T1,T2| = sqrt( d2 - ri2).
L'angle α = atan(ri/t). ou α = asin(ri/d).
|
La calulation de la longueur de la ceinture autour le deux cercles :
La longueur du segment de cercle autour du cercle C1 :
l1 = 2π·r1 ·(180+2·α)/360.
La longueur du segment de cercle autour du cercle C2:
l2 = 2π·r2 ·(180-2·α)/360.
La longueur de la ceinture complète :
l = l1 + l2 + 2·t .
|
|
Tangentes externes aux deux Cercles rendu avec POV-Ray
|
|
À quoi est util cette géométrie ?
Ici quelques exemples :
|
|
|
Un tore conique arrondi.
|
Un prisme conique arrondi.
|
|
|
|
|
|
| top
|
|