Home
- POV-Ray Tutorial
- Geometrie Grundlagen
für Raytracing
Rechtwinkliges Dreieck
Pythagoras
Trigonometrie Basis
Kosinussatz
Gleichseitiges Dreieck
Reguläres Polygon
Polyeder
Regulärer Tetraeder
Regulärer Oktaeder
Würfel & Quader
Regulärer Dodekaheder
Regulärer Ikosaeder
Kuboktaeder
Oktaederstumpf
Rhombenkuboktaeder
Ikosaederstumpf
Kreise
Tangierende Kreise
Interne Tangenten
Externe Tangenten
- Geometric 3D Animations
|
Externe Tangenten zweier Kreise
Im folgenden wird für die Quadratwurzel einer Zahl, der englische Ausdruck "sqrt(ZAHL)"
gemäß der von POV-Ray verwendeten Syntax geschrieben.
Anmerkung: Hier werden Objekte der 2D-Geometrie durch 3D-Objekte in der xy-Ebene dargestellt.
Daher müssen alle Koordinaten die z-Komponente Null haben! ( <?,?,0>) |
|
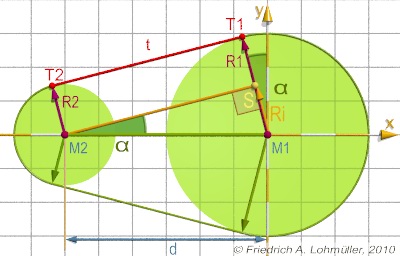
Wir suchen die externe Tangente zu den Berührungspunkten
T1 und T2 von zwei Kreisen C1(M1,r1) und
C2(M2,r2) mit
den Radien r1 > r2 ,
wie in nebenstehender Abbildung.
Der Abstand der Mittelpunkte ist d.
Der Unterschied der Radien ist ri = r1 - r2.
|
Das Dreieck M1,S,M2 hat einen rechten Winkel bei S.
Die Strecke(T1,T2) ist parallel zur Strecke(M2,S) und hat dieselbe Länge.
Daher gilt t = |T1,T2| = sqrt( d2 - ri2).
Der Winkel α = atan(ri/t). oder α = asin(ri/d).
|
Die Berechnung der Länge des gesamten Gürtels:
Die Länge des Segments um den Kreis C1:
l1 = 2π·r1 ·(180+2·α)/360.
Die Länge des Segments um den Kreis C2:
l2 = 2π·r2 ·(180-2·α)/360.
Die gesamte Länge des Gürtels ist:
l = l1 + l2 + 2·t .
|
|
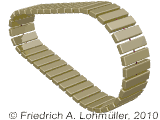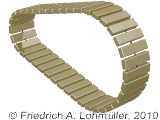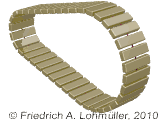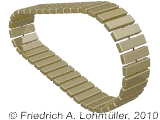
Externe Tangenten an zwei Kreise gerendert mit POV-Ray
|
|
Wozu kann man diese Geometrie gebrauchen?
Hier einige Beispiele:
|
|
|
Ein konische runder Torus.
|
Ein konische rundes Prisma.
|
|
|
|
|
|
| top
|
|