Deux cylindres fondus

//---------------------------------------
#macro Two_Cylinder_Blob_0(
           Pitch, // distance of centers
           SD,    // slice thickness in z
           Cyl_R, // cylinder radius
           Fillet_R , // fillet radius
           Axis_R, // <Cyl_R, 0=non
        ) //-----------------------------
//---------------------------------------
#local D = 0.00001; // a little bit
// distance of fillet from centerline
// of right and left cylinder:
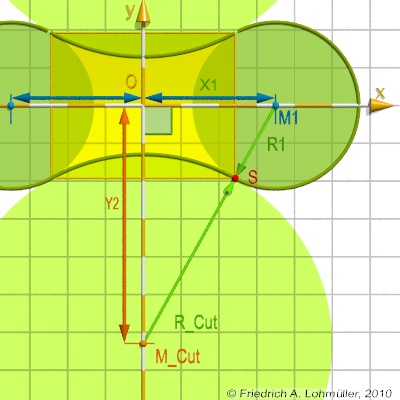
#local Fillet_Y  =
  sqrt( pow(Fillet_R+Cyl_R,2)
  - pow(Pitch/2,2));
// S = tangent point of the cylinders!
// proportional!
#local S_X =
 Fillet_R/(Cyl_R + Fillet_R)*Pitch;
#local S_Y =
Cyl_R/(Cyl_R + Fillet_R)*Fillet_Y;
//---------------------------------------
#if (Axis_R > 0)
difference{
#end //----------------------------------
union{
 cylinder{ <0,0,-SD/2>,<0,0,SD/2>,Cyl_R
           translate< Pitch/2,0,0>}
 cylinder{ <0,0,-SD/2>,<0,0,SD/2>,Cyl_R
           translate<-Pitch/2,0,0>}
 difference{ // 2
  box{<-S_X,-S_Y,-SD/2>,<S_X,S_Y,SD/2> }
  cylinder{ <0,0,-SD/2-D>,
            <0,0,SD/2+D>, Fillet_R
            translate<0, Fillet_Y,0>}
  cylinder{ <0,0,-SD/2-D>,
            <0,0,SD/2+D>, Fillet_R
            translate<0,-Fillet_Y,0>}
 } // end difference 2
} // end union -------------------------
#if (Axis_R > 0)
cylinder{<0,0,-SD-D>,<0,0,SD/2+D>,Axis_R
         translate< Pitch/2,0,0>}
cylinder{<0,0,-SD-D>,<0,0,SD/2+D>,Axis_R
         translate<-Pitch/2,0,0>}
} // end of difference or union
#end // of 'Axis_R > 0'
#end //--------------------- end of macro
//---------------------------------------

// example://----------------------------
object{ Two_Cylinder_Blob_0 (
          0.0127, // Pitch distance
          0.0009, // slice thickness
          0.0051, // cylinder radius
          0.0081, // fillet radius
          0.0022, // axis r,
           //< cylinder r, 0=non
         )//-----------------------------
        texture{
           pigment{ color rgb<1,1,1>}
           finish { phong 1.0}
        } // end of texture
        rotate<0,0,0>
        translate<0,0,0>
      } // end of sphere ----------------
//---------------------------------------