La Forme d'une Fiole
de Ballon monocol

La construction d'un ballon monocol. Une combination d'une boule et un cylindre avec une moulure concave à la base du goulot de la fiole.
Objets:   "box", "sphere", "cylinder" "torus".
Méthodes: "#declare","union", "intersection" "#macro".
Cliquez ici pour un exemple!

La Construction de la forme d'un ballon monocol.
Une vue en coupe de la géométrie de cette construction on peut voir dans l'image ci-contre.
( Pour plus de détails de la géométrie élémentaire
  voir ici: Cercles touchants.)

Pour obtenir une moulure concave parfaitement arrondi à la base du goulot nous devons calculer la distance entre le tore pour la moulure et la sphère de la boule. Aussi les coordonnées du point S sont necessaire pour la largheur et la hauteur de le cylindre central de la moulure de quelle le tore doit être soustrait.
Pour permettre aussi des matèrials transparentes come verre nous avons besoin de utiliser optionnellement 'merge' au lieu de 'union'.

// -----------------------------------------
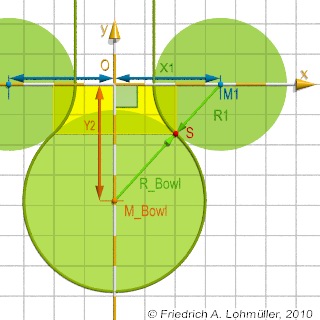
#local M1 = <Fillet_R+Neck_R,0,0>;
#local Y2 =
 sqrt( pow(Fillet_R+Bowl_R,2)-pow(M1.x,2) );
#local M2 = <0,-Y2,0>;

#local XS = M1.x*Bowl_R/(Fillet_R+Bowl_R);
#local YS = M2.y*Fillet_R/(Fillet_R+Bowl_R);
#local S = <XS,YS,0>;
// --------------------------------------
// calculation of real height
#declare Total_Height =
 Y2 + Bowl_R + Neck_L;
//---------------------------------------
// base shape ---------------------------
#if ( Merge_On = 1) merge{
#else               union{
#end
 difference{
  cylinder{<0,0,0>,<0,S.y,0>,S.x}
  torus{ M1.x, Fillet_R }
 }// end diff
 sphere{ M2, Bowl_R }
 // neck --------------------------------
 #if (Neck_L > 0)
 cylinder{<0,-D,0>, <0,Neck_L,0>,Neck_R}
 #end // of "#if( Neck_L > 0 )"
 //--------------------------------------
 translate<0,-M2.y+Bowl_R,0>
} // end of union or merge -----------------