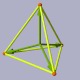
Propriétés Géométriques de Base du Tétraèdre
utiliser ici :
Pour plus de details voir Géométrie du Tétraèdre régulier.
Avec la longueur du côté "Side_a" de un tétraèdre régulier
nous pouvons calculer le rayon de la sphère circonscrite :
R_circum = sqrt( 3/8 ) * Side_a;
et l'angle entre sommet, centre et un autre sommet :
Vertex_Center_Vertex_Angle = degrees(acos(-1/3)); (~ 109.471).
Nous commencons avec la déclaration de la longueur du côté "Side_a" :
#declare Side_a = 1;
#declare R_circum = sqrt( 3/8 ) * Side_a;
#declare Vertex_Center_Vertex_Angle = degrees( acos( -1/3 )); |
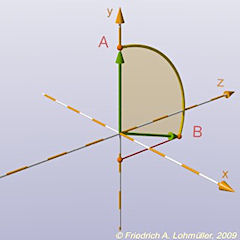
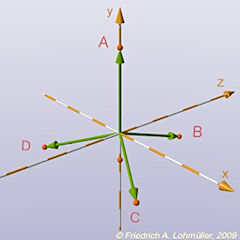
Les vecteurs V1,V2,V3,V4 de <0,0,0> àux sommets A,B,C,D :
// caculation of the vectors --------------------------------
#declare V1 = <0,R_circum,0>;
#declare V2 = vrotate( V1,< Vertex_Center_Vertex_Angle,0,0>);
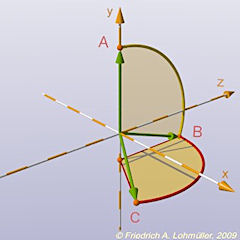
#declare V3 = vrotate( V2,< 0, 120, 0>);
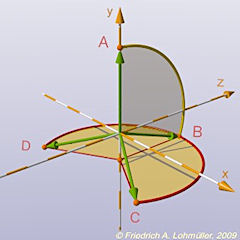
#declare V4 = vrotate( V2,< 0,-120, 0>);
//----------------------------------------------------------- |
Pour représenter les symboles des vecteurs nous utilisons la macro suivante :
//---------------------------- macro Vector(Start,End,Radius)
#macro Vector(P_s,P_e, Rv)
union{
cylinder{ P_s, P_e - (vnormalize(P_e - P_s)*9.5*Rv), Rv }
cone { P_e - (vnormalize(P_e - P_s)*10*Rv), 3*Rv, P_e,0}
}// end of union
#end //----------------------------------------- end of macro |
Alternatif : #include "analytical_g.inc"
pour dessiner vecteurs du centre àux sommets:
#declare Vector_Texture =
texture{ pigment{ color rgb<0.2,0.5,0.0>}
finish { phong 1} }
#declare Rl = 0.01; // line radius
// vectors --------------------------------------------------
object{ Vector( o,V1, Rl) texture{ Vector_Texture }}
object{ Vector( o,V2, Rl) texture{ Vector_Texture }}
object{ Vector( o,V3, Rl) texture{ Vector_Texture }}
object{ Vector( o,V4, Rl) texture{ Vector_Texture }}
//----------------------------------------------------------- |
Si nous déclarons les textures correspondantes in une manière analogue,
nous pouvons dessiner
les sommets, les côtés et les faces :
#declare Corners_Texture =
texture{ pigment{ color rgb<0.75,0.1,0.0>}
finish { phong 1} }
#declare Edge_Texture =
texture{ pigment{ color rgb<1,0.5,0.0>}
finish { phong 1} }
#declare Surface_Texture =
texture{ pigment{ color rgbt<0.3,0.7,0.0, 0.75>}
finish { phong 1} }
#declare Rp = 0.025; // 'point' radius
// corners ------------------------------------------
sphere{ V1, Rp texture{ Corners_Texture } }
sphere{ V2, Rp texture{ Corners_Texture } }
sphere{ V3, Rp texture{ Corners_Texture } }
sphere{ V4, Rp texture{ Corners_Texture } }
// edges --------------------------------------------
cylinder{ V1, V2, Rl texture{ Edge_Texture } }
cylinder{ V2, V3, Rl texture{ Edge_Texture } }
cylinder{ V3, V1, Rl texture{ Edge_Texture } }
cylinder{ V1, V4, Rl texture{ Edge_Texture } }
cylinder{ V2, V4, Rl texture{ Edge_Texture } }
cylinder{ V3, V4, Rl texture{ Edge_Texture } }
// surfaces------------------------------------------
triangle{ V1, V2, V3 texture{ Surface_Texture } }
triangle{ V1, V2, V4 texture{ Surface_Texture } }
triangle{ V2, V3, V4 texture{ Surface_Texture } }
triangle{ V3, V1, V4 texture{ Surface_Texture } }
//--------------------------------------------------- |
|
Pas 1: pivoter VA sur l'axe x avec 109.47°.
Pas 2: pivoter VB sur l'axe y avec +120°.
Pas 3: pivoter VB sur l'axe y avec -120°.
Les vecteurs des sommet du tétraèdre.
Désciption de la scène pour POV-Ray:
"Regular_Tetrahedron_Vectors_1.pov" ou
"Regular_Tetrahedron_Vectors_1.txt"
|