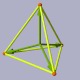
Elementare geometrische Eigenschaften des Tetraeders
welche hier verwendet werden:
Für mehr Details siehe Elementare Geometrie des reguläre Tetraeders.
Aus der Seitenlänge "Side_a" eines regulären Tetraeders kann man
den Radius der Umkugel (berührt alle Eckpunkte/Scheitel) berechnen:
R_circum = sqrt( 3/8 ) * Side_a;
und den Winkel zwischen einem Scheitel, dem Mittelpunkt und einem anderen Scheitel:
Vertex_Center_Vertex_Angle = degrees(acos(-1/3)); (~ 109.471).
Wir beginnen mit der Deklaration der Seite des Tetraeders "Side_a":
#declare Side_a = 1;
#declare R_circum = sqrt( 3/8 ) * Side_a;
#declare Vertex_Center_Vertex_Angle = degrees( acos( -1/3 )); |
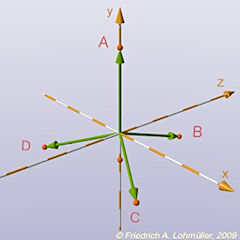
Die Vektoren V1,V2,V3,V4 von <0,0,0> zu den Ecken A,B,C,D:
// caculation of the vectors --------------------------------
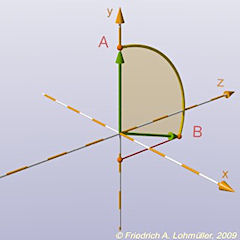
#declare V1 = <0,R_circum,0>;
#declare V2 = vrotate( V1,< Vertex_Center_Vertex_Angle,0,0>);
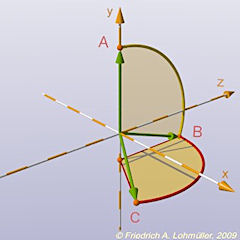
#declare V3 = vrotate( V2,< 0, 120, 0>);
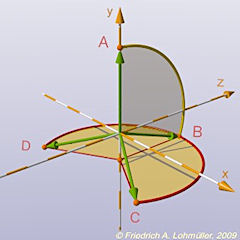
#declare V4 = vrotate( V2,< 0,-120, 0>);
//----------------------------------------------------------- |
Zum Darstellen der Vektorsymbole verwenden wir das folgende Makro:
//---------------------------- macro Vector(Start,End,Radius)
#macro Vector(P_s,P_e, Rv)
union{
cylinder{ P_s, P_e - (vnormalize(P_e - P_s)*9.5*Rv), Rv }
cone { P_e - (vnormalize(P_e - P_s)*10*Rv), 3*Rv, P_e,0}
}// end of union
#end //----------------------------------------- end of macro |
Alternativ: #include "analytical_g.inc"
zum Zeichnen der Vektoren zu den Ecken:
#declare Vector_Texture =
texture{ pigment{ color rgb<0.2,0.5,0.0>}
finish { phong 1} }
#declare Rl = 0.01; // line radius
// vectors --------------------------------------------------
object{ Vector( o,V1, Rl) texture{ Vector_Texture }}
object{ Vector( o,V2, Rl) texture{ Vector_Texture }}
object{ Vector( o,V3, Rl) texture{ Vector_Texture }}
object{ Vector( o,V4, Rl) texture{ Vector_Texture }}
//----------------------------------------------------------- |
Wenn wir die entsprechenden Texturen in analoger Weise deklarieren können wir
die Ecken, Kanten und Flächen darstellen:
#declare Corners_Texture =
texture{ pigment{ color rgb<0.75,0.1,0.0>}
finish { phong 1} }
#declare Edge_Texture =
texture{ pigment{ color rgb<1,0.5,0.0>}
finish { phong 1} }
#declare Surface_Texture =
texture{ pigment{ color rgbt<0.3,0.7,0.0, 0.75>}
finish { phong 1} }
#declare Rp = 0.025; // 'point' radius
// corners ------------------------------------------
sphere{ V1, Rp texture{ Corners_Texture } }
sphere{ V2, Rp texture{ Corners_Texture } }
sphere{ V3, Rp texture{ Corners_Texture } }
sphere{ V4, Rp texture{ Corners_Texture } }
// edges --------------------------------------------
cylinder{ V1, V2, Rl texture{ Edge_Texture } }
cylinder{ V2, V3, Rl texture{ Edge_Texture } }
cylinder{ V3, V1, Rl texture{ Edge_Texture } }
cylinder{ V1, V4, Rl texture{ Edge_Texture } }
cylinder{ V2, V4, Rl texture{ Edge_Texture } }
cylinder{ V3, V4, Rl texture{ Edge_Texture } }
// surfaces------------------------------------------
triangle{ V1, V2, V3 texture{ Surface_Texture } }
triangle{ V1, V2, V4 texture{ Surface_Texture } }
triangle{ V2, V3, V4 texture{ Surface_Texture } }
triangle{ V3, V1, V4 texture{ Surface_Texture } }
//--------------------------------------------------- |
|
Schritt 1: rotieren von VA um die x-Achse um 109.47°.
Schritt 2: rotieren von VB um die y-Achse um +120°.
Schritt 2: rotieren von VB um die y-Achse um -120°.
Die Vektoren der Eckpunkte des Tetraeders.
Szenenbeschreibung für POV-Ray:
"Regular_Tetrahedron_Vectors_1.pov" oder
"Regular_Tetrahedron_Vectors_1.txt"
|