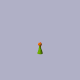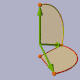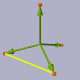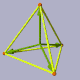Dimensionen
Länge der Tetraeder-Kante: a. |
Die Höhe
eines regulären Tetraeders:
h = sqrt (2/3) * a ;
Der Radius der Umkugel:
R = sqrt( 3/8 ) * a ;
Die Höhe des Mittelpunktes der Inkugel oder
der Radius der Inkugel:
r = 1/3 * R oder
r = 1/sqrt(24) * a ;
Der Radius der Zwischenkugel (tangiert die Kanten):
rm = 1/sqrt(8) * a ;
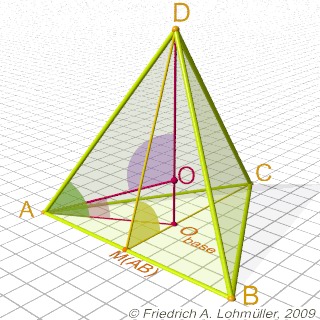
Der Winkel zwischen 2 Flächen: ~ 70,53 (yellow)
Winkel(C,MAB,D) = degrees(atan(2*sqrt(2)));
Der Winkel zwischen Kante und Fläche: ~ 54,74 (green)
Winkel(0,A,D) = degrees( atan(sqrt(2)));
Der Winkel Ecke-Mittelpunkt-Ecke: ~ 109.471 (violet)
Winkel(A,0,D) = degrees( acos( -1/3 ));
|
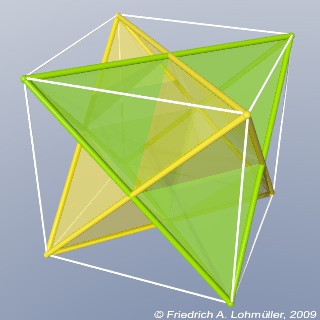
Zwei reguläre Tetraeder im Würfel
|
Ein regulärer Tetraeder
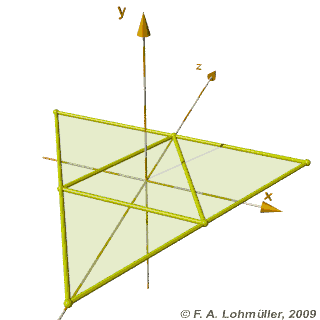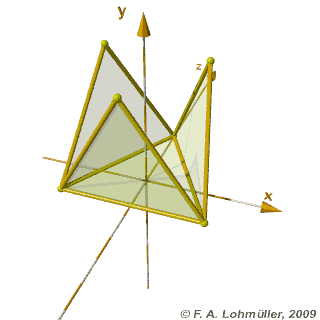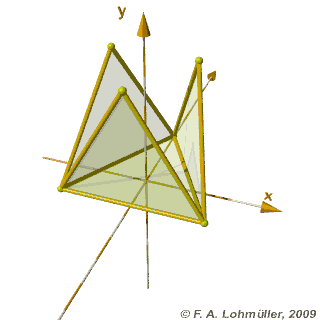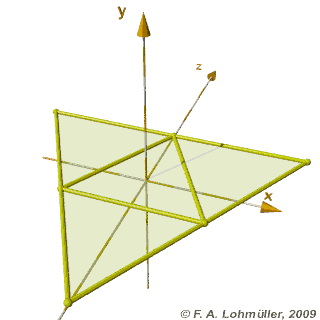
Faltung eines regulären Tetraeders
Ein Tetraeder aus Vektoren
Wie man das mit POV-Ray macht.
Animation mit POV-Ray
|