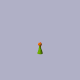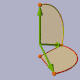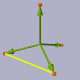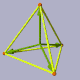Les Dimensions
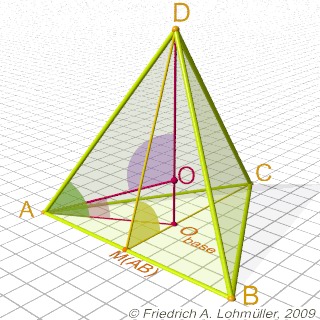
Longueur d'un côté de base du triangle: a.
|
L'hauteur d'un
tétraèdre régulier :
h = sqrt (2/3) * a ;
Le rayon de la sphère circonscrite :
R = sqrt( 3/8 ) * a ;
L'hauteur du centre O de la sphère inscrite ou
le rayon de la sphère inscrite :
r = 1/3 * R or
r = 1/sqrt(24) * a ;
Le rayon del'entresphère (arêtes = tangentes) :
rm = 1/sqrt(8) * a ;
L'angle entre deux faces : ~ 70,53 (yellow)
Angle(C,MAB,D) = degrees(atan(2*sqrt(2)));
L'angle entre une arête et une face : ~ 54,74 (green)
Angle(0,A,D) = degrees( atan(sqrt(2)));
L'angle entre sommet, centre et sommet : ~ 109.471 (violet)
Angle(A,0,D) = degrees( acos( -1/3 ));
|
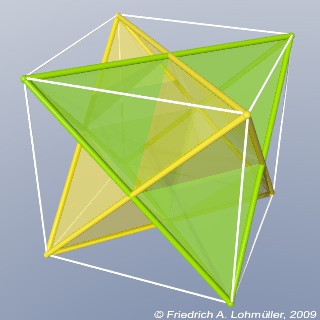
Deux tétraèdres réguliers dans un cube
|
Un tétraèdre régulier
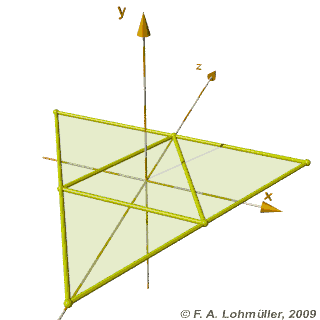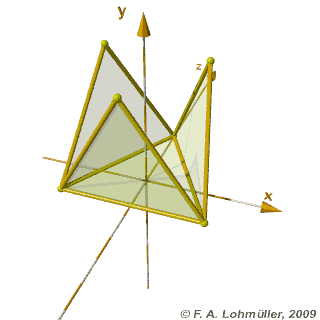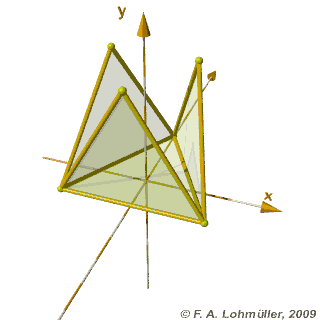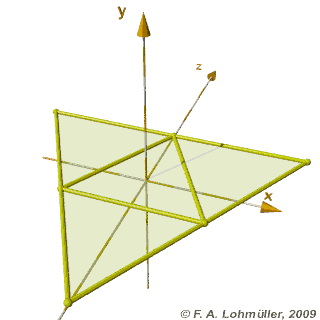
Pliage et dépliage d'un tétraèdre régulier
Un tétraèdre de vecteurs
Comment faire avec POV-Ray
Animation en POV-Ray
|