Beschreibungen und Beispiele zum Raytracer POV-Ray
von Friedrich A. Lohmüller
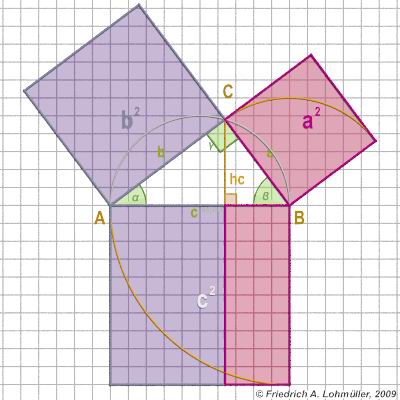
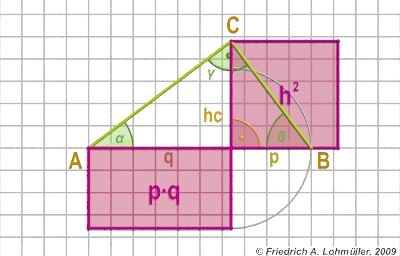
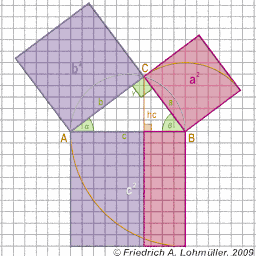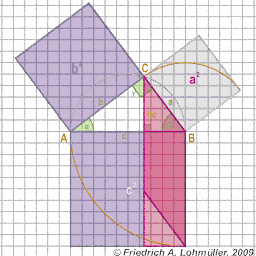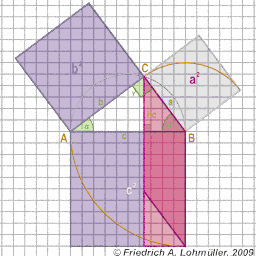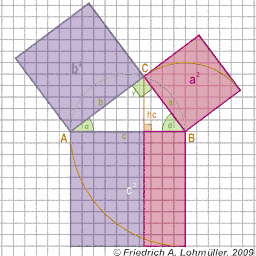
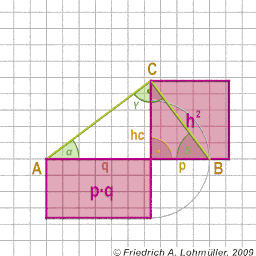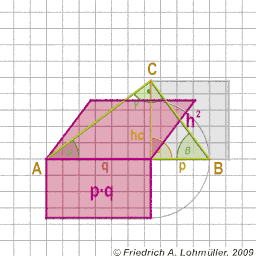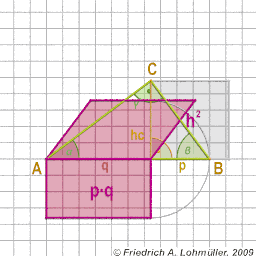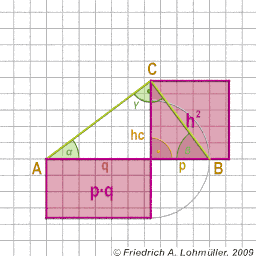
Elementare Geometrie
für Raytracing
Italiano
Français