Home
- POV-Ray Tutorial
- Geometrie Grundlagen
für Raytracing
Rechtwinkliges Dreieck
Pythagoras
Trigonometrie Basis
Kosinussatz
Gleichseitiges Dreieck
Reguläres Polygon
Polyeder
Regulärer Tetraeder
Regulärer Oktaeder
Würfel & Quader
Regulärer Dodekaheder
Regulärer Ikosaeder
Kuboktaeder
Oktaederstumpf
Rhombenkuboktaeder
Ikosaederstumpf
Kreise
Tangierende Kreise
Interne Tangenten
Externe Tangenten
- Geometric 3D Animations
|
| |
Das reguläre Polygon
Ein reguläres Polygon ist ein Vieleck das gleiche Innenwinkel und gleiche Seiten hat.
Das gleichseitige Dreieck (3), das Quadrat (4), das reguläre Pentagon (5), das Hexagon (6), das Heptagon (7),
das Oktagon (8), das Enneagon (9), das Dekagon (10), das Hendekagon (11), das Dodekagon (12), ... ,
das Hektagon (100), das Chiliagon (1000), das Miriagon (10000), das Megagon (1000000),
das Gigagon (1000 000 000), das Teragon (1000 000 000 000 000 000),
das Petagon (1000 000 000 000 000 000 000), ... , der Kreis (∞).
|
Anmerkung: Die trigonometrischen Funktionen sin(X), cos(X) und tan(X) benötigen in POV-Ray
ihre Argumente für den Winkel X in Bogenmaß (radians) !!! Das Symbole π = pi in POV-Ray.
|
Ein reguläres Polygon mit N Ecken oder N Seiten:
Die Summe der Innenwinkel = 180*(N-2);
Der Innenwinkel = 180-360/N;
gleichseitiges Dreieck: 180-360/3 = 180 - 120 = 60;
Quadrat: 180-360/4 = 180 - 90 = 90;
reguläres Pentagon: 180-360/5 = 180 - 72 = 108;
reguläres Hexagon: 180-360/6 = 180 - 60 = 120;
reguläres Heptagon: 180-360/7 = 180-51,43 = 128,57;
reguläres Oktagon: 180-360/8 = 180 - 45 = 135;
reguläres Enneagon: 180-360/9 = 180 - 40 = 140;
reguläres Dekagon: 180-360/10= 180 - 36 = 144;
reguläres Hendekagon: 180-360/11= 180 -32,7 = 147,3;
reguläres Dodekagon: 180-360/12= 180 - 30 = 150; |
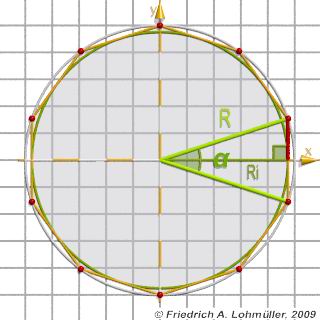
Ein reguläres Polygon mit N Ecken und
mit dem Umkreisradius R,
oder mit dem Inkreisradius Ri:
Die Länge der Seite a:
a = 2* R * sin( radians( 180/N ) ); oder
a = 2*R *sin( pi/N );
a = 2* Ri * tan( radians( 180/N ) ); oder
a = 2*Ri*tan( pi/N );
|
Mit der Länge der Seite a eines regulären Polygons:
Der Radius des Umkreises:
R = 1/2 * a/sin( radians( 180/N ) ) ); o
R = 1/2 * a/sin( pi/N );
Der Radius des Inkreises:
Ri = 1/2 * a/tan( radians( 180/N ) ) ); o
Ri = 1/2 * a/tan( pi/N );
|
|
Das reguläre Polygon - Winkel, Seiten, Radien.
|
|