Home
- POV-Ray Tutorial
- Geometrie Grundlagen
für Raytracing
Rechtwinkliges Dreieck
Pythagoras
Trigonometrie Basis
Kosinussatz
Gleichseitiges Dreieck
Reguläres Polygon
Polyeder
Regulärer Tetraeder
Regulärer Oktaeder
Würfel & Quader
Regulärer Dodekaheder
Regulärer Ikosaeder
Kuboktaeder
Oktaederstumpf
Rhombenkuboktaeder
Ikosaederstumpf
Kreise
Tangierende Kreise
Interne Tangenten
Externe Tangenten
- Geometric 3D Animations
|
Der Kosinussatz
Einige nützliche geometrische Tatsachen über Winkel und Seiten beliebiger Dreiecke. |
Anmerkung: Die trigonometrischen Funktionen sin(X), cos(X) und tan(X) benötigen in POV-Ray
ihre Argumente für den Winkel X in Bogenmaß (radians) !!! Das Symbole π = pi in POV-Ray.
Entsprechend ergeben die Umkehrfunktionen asin(x), acos(x) und atan(x) die entsprechenden Winkel im Bogenmaß.
|
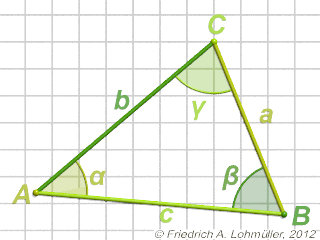
Für jedes Dreieck ABC gilt:
c2 = a2 + b2 - 2*a*b*cos( γ ) (1)
b2 = a2 + c2 - 2*a*c*cos( β ) (2)
a2 = b2 + c2 - 2*b*c*cos( α ) (3)
Für γ = 90° = pi/2 (rechtwinkliges Dreieck)
ergibt sich cos(γ) = 0 und damit aus (1):
c2 = a2 + b2 (Satz des Pythagoras).
-----------------------------------------------------
Für die Winkel eines Dreiecks ABC
ergeben sich damit folgende Formeln:
γ = acos ( ( a2 + b2 - c2 )/(2*a*b) ) (4)
β = acos ( ( a2 + c2 - b2 )/ (2*a*c) ) (5)
α = acos ( ( b2 + c2 - a2 )/ (2*b*c) ) (6)
|
|
Ein bliebiges Dreieck 2D.
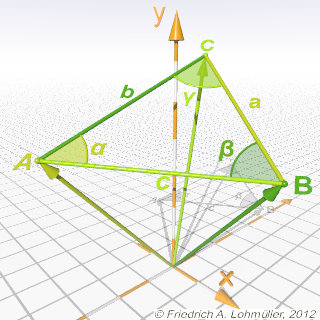
Ein bliebiges Dreieck 3D.
|
|
|
|