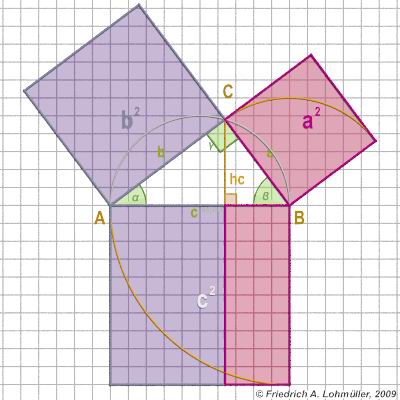
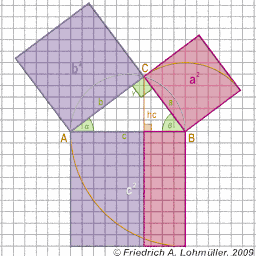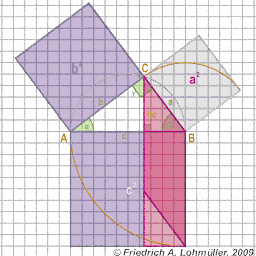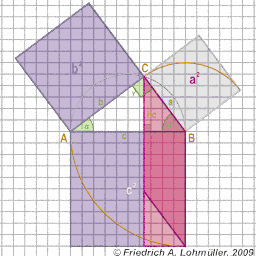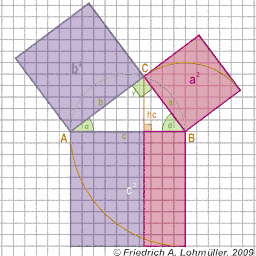
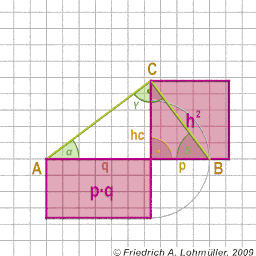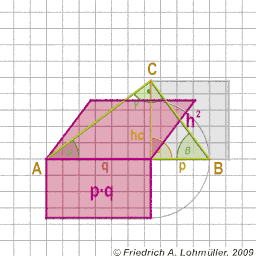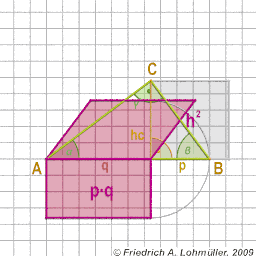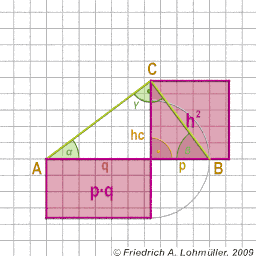
In un triangolo rettangolo
con la ipotenusa c,
e i cateti a e b
vale il teorema di Pitagora:
a2 + b2 = c2
(In ogni triangolo rettangolo,
l'area del quadrato costruito sull'ipotenusa è equivalente
alla somma delle aree dei quadrati costruiti sui cateti.)
|
Il calcolo dei lati:
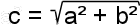
c = sqrt( a*a + b*b ) ; o
c = sqrt( pow( a , 2) + pow( b , 2 ) ) .
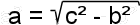
a = sqrt( c*c - b*b ) ;
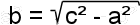
b = sqrt( c*c - a*a ) ;
|
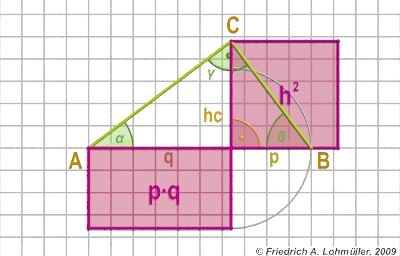
1° teorema di Euclide sui cateti a e b:
a2 = p*c or
b2 = q*c
|
2° teorema di Euclide su altezza hc:
h2 = p * q
|
|
Il teorema di Pitagora al triangolo rettangolo
Il 2° teorema di Euclide: h2 = p * q
|