Home
- POV-Ray Tutorial
- Geometrie Grundlagen
für Raytracing
Rechtwinkliges Dreieck
Pythagoras
Trigonometrie Basis
Kosinussatz
Gleichseitiges Dreieck
Reguläres Polygon
Polyeder
Regulärer Tetraeder
Regulärer Oktaeder
Würfel & Quader
Regulärer Dodekaheder
Regulärer Ikosaeder
Kuboktaeder
Oktaederstumpf
Rhombenkuboktaeder
Ikosaederstumpf
Kreise
Tangierende Kreise
Interne Tangenten
Externe Tangenten
- Geometric 3D Animations
|
Das rechtwinklige Dreieck |
Anmerkung: Um eine Kollision mit fest vordefinierten Bezeichnern und in POV-Ray reservierten Wörter zu vermeiden,
wird dringend empfohlen, als Bezeichner für Variable und Objekte, welche vom Benutzer definiert werden,
nur Wörter zu verwenden, die mit einem Großbuchstaben beginnen.
D.h. man verwende "Ri" anstatt "r"
und man verwende "H" anstelle von "h".
|
Dimensionen
Die längste Seite, die Seite gegenüber dem rechten Winkel γ bei Punkt C,
wird als Hypotenuse c bezeichnet,
die beiden anderen Seiten werden als Katheten (singular: Kathete) a und b bezeichnet.
Der Innenwinkel α ist bei A und
der Innenwinkel ϐ ist bei B.
|
α + ϐ = 90 Grad.
Der Radius des Umkeises R:
Mit d(A,B) = Abstand zwischen A und B gilt
R = 1/2 * c = 1/2* d(A,B);
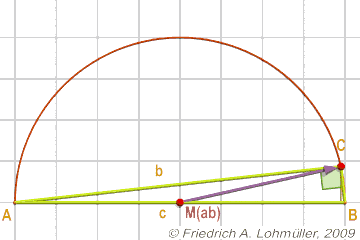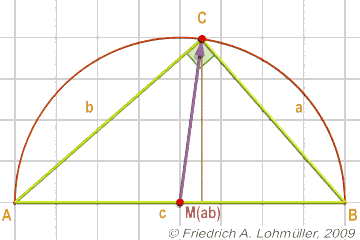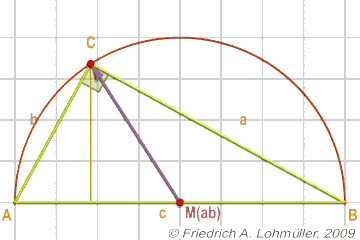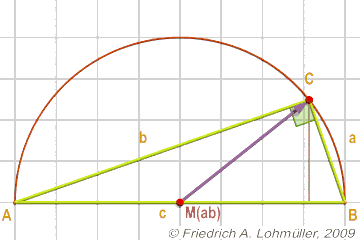
Der Satz des Thales
und die Seitenhalbierende sc: (violet in Animation!)
In jedem rechtwinkligen Dreieck gilt:
Die Seitenhalbierende sc der Seite c
(gegenüber dem rechten Winkel)
hat die Länge 1/2 * c.
Andererseits:
Jedes Dreieck, bei dem der Punkt C auf einem Halbkreis
über der gegenüberliegenden Seite liegt,
ist ein rechtwinkliges Dreieck.
|
|
Ein rechtwinkliges Dreieck.
Ein rechtwinkliges Dreieck und der Satz des Thales,
Seitenhalbierence sc und Thaleskreis.
|
|
|
|