Home
- Tutorial POV-Ray
- Geometria di Base
per Raytracing
Triangolo Rettangolo
Teorema di Pitagora
Trigonometria di Base
Teorema del Coseno
Triangolo Equilatero
Poligono Regulare
Poliedro
Tetraedro Regolare
Ottaedro Regolare
Cubo e Cuboide
Dodecaedro Regolare
Icosaedro Regolare
Cubottaedro
Ottaedro troncato
Rombicubottaedro
Icosaedro troncato
Cerchi
Cerchi tangenti
Tangenti interne
Tangenti esterne
- Animazioni Geometriche 3D
|
Nota: Per evitare collisioni con denominazioni installate e parole riservate di POV-Ray,
si è racommandato assolutamente di usare solo parole con una maiuscola come lettera iniziale,
per tutte denominazioni di variabili e oggetti dichiarrate degli utenti, per es. si usa "Ri" invece di "r"
e si usa "H" invece di "h".
|
Dimensions and Names
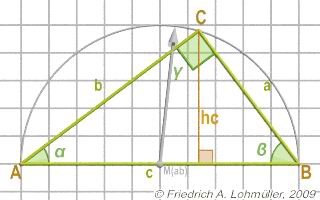
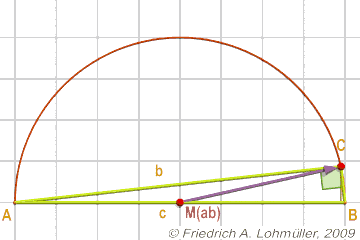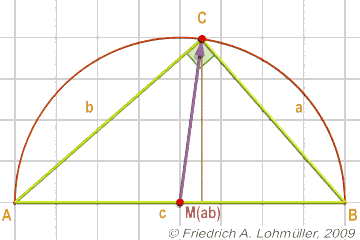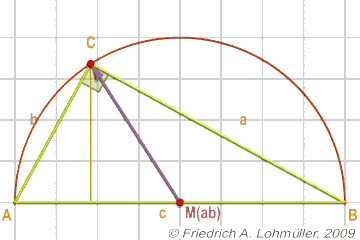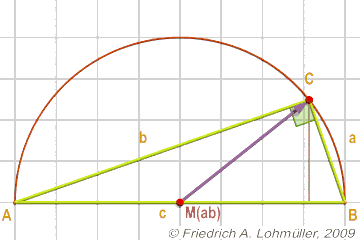
Il lato più lungo è opposto all'angolo retto γ al punto C.
Questo lato si chiama ipotenusa c,
I altri due late si chiama cateti a e b.
L'angolo α si trova a A e l'angolo ϐ e l'angolo a B. |
α + ϐ = 90 degrees.
Il raggio del circumcerchio:
R = 1/2 * c = 1/2* d(A,B);
La regola della mediana:
Per un triangolo rettangolo:
Si MAB è la media della ipotenusa c,
poi CMAB = ½ c.
Si può anche dire che il punto C si trova su un cherchio con il diametro [AB].
Ou inversamente detto: Si C è un punto su un cherchio con il diametro [AB],
poi l'angolo C nel triangolo ABC è un angolo retto.
|
|
Un triangolo rettangolo
Un triangolo rettangolo e il "Thales’ Theorem",
il teorema dell’angolo retto inscritto nella semi-circonferenza.
|
|
|
|