Home
- Tutorial POV-Ray
- Geometria di Base
per Raytracing
Triangolo Rettangolo
Teorema di Pitagora
Trigonometria di Base
Teorema del Coseno
Triangolo Equilatero
Poligono Regulare
Poliedro
Tetraedro Regolare
Ottaedro Regolare
Cubo e Cuboide
Dodecaedro Regolare
Icosaedro Regolare
Cubottaedro
Ottaedro troncato
Rombicubottaedro
Icosaedro troncato
Cerchi
Cerchi tangenti
Tangenti interne
Tangenti esterne
- Animazioni Geometriche 3D
|
Trigonometria di Base
sin, cos, tan - Qualche fondamento geometrico molto utile
sulle funzioni trigonometriche seno, coseno e tangente. |
Nota: Per le funzioni trigonometriche sin(X), cos(X) and tan(X) in POV-Ray
dobbiamo avere il argumento X espresso in radianti !!!
Il simbolo π = pi in POV-Ray.
|
L'unità degli angoli: gradi e radiante
Un angolo misurato in gradi: simbolo "°"
Un angolo misurato con la lunghezza di un arco: simbolo "rad",
di sovente in parte di "pi".
(360° = 2*pi; 180° = pi) |
Conversione di un valore in radianti value RadVal
in un valore corrispondente in gradi DegVal:
#declare DegVal = degrees(RadVal); or
#declare DegVal = RadVal*(180/pi);
Conversione di un valore in gradi DegVal in un valore corrispondente in radianti RadVal:
#declare RadVal = radians(DegVal); or
#declare RadVal = DegVal*(pi/180);
Si abbiamo il valore di un angolo A in gradi:
#declare SineVal = sin(radians( A ));
L'equivalente vale anche per i funzioni inverse asin, acos e atan in POV-Ray:
Si vogliamo un valore del angolo A in gradi:
#declare Angle_in_deg = degrees( asin( 0.50 ));
Altrimenti otteniamo il valore misurato in radianti:
#declare Angle_in_rad = asin( 0.50 ) ;.
|
|
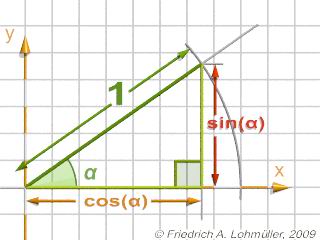
Seno e coseno in un triangolo rettangolo
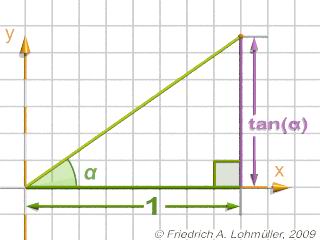
Tangente in un triangolo rettangolo
|
|
|
|