Home
- Tutorial POV-Ray
- Geometria di Base
per Raytracing
Triangolo Rettangolo
Teorema di Pitagora
Trigonometria di Base
Teorema del Coseno
Triangolo Equilatero
Poligono Regulare
Poliedro
Tetraedro Regolare
Ottaedro Regolare
Cubo e Cuboide
Dodecaedro Regolare
Icosaedro Regolare
Cubottaedro
Ottaedro troncato
Rombicubottaedro
Icosaedro troncato
Cerchi
Cerchi tangenti
Tangenti interne
Tangenti esterne
- Animazioni Geometriche 3D
|
| |
Poligono Regolare
Un poligono regolare è un poligono in cui tutti i lati e tutti gli angoli sono uguali.
Il triangolo equilatero (3), il quadrato (4), il pentagono regolare (5), il esagono regolare (6), il ettagono (7),
il ottagono (8), il ennagono (9), il decagono (10), il endecagono (11), il dodecagono (12), ... ,
il chiliagon (1000), il miriagono (10000), il megagono (1000000), il gigagono (1000 000 000),
il teragono (1000 000 000 000 000 000), il petagono (1000 000 000 000 000 000 000), ...
, il cherchio (∞).
|
Nota: Per le funzioni trigonometriche sin(X), cos(X) and tan(X) in POV-Ray
dobbiamo avere il argumento X espresso in radianti !!!
Il simbolo π = pi in POV-Ray.
|
In un poligono regolare con N angoli o N lati:
La somma degli angoli interni = 180*(N-2);
L'angolo interno = 180-360/N;
triangolo equilatero: 180-360/3 = 180 - 120 = 60;
quadrato: 180-360/4 = 180 - 90 = 90;
pentagono regolare: 180-360/5 = 180 - 72 = 108;
esagono regolare: 180-360/6 = 180 - 60 = 120;
ettagono regolare: 180-360/7 = 180-51,43 = 128,57;
ottagono regolare: 180-360/8 = 180 - 45 = 135;
ennagono regolare: 180-360/9 = 180 - 40 = 140;
decagono regolare: 180-360/10= 180 - 36 = 144;
endecagono regolare: 180-360/11= 180 -32,7 = 147,3;
dodecagono regolare: 180-360/12= 180 - 30 = 150; |
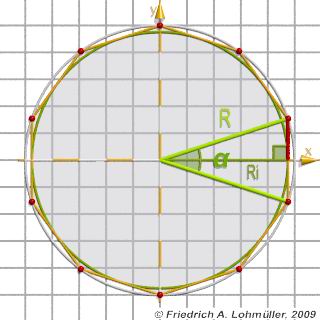
Un poligono regolare con N angoli e
con il raggio del circumcerchio R,
o con il raggio del incerchio Ri:
La lunghezza del lato a:
a = 2* R * sin( radians( 180/N ) ); o
a = 2*R *sin( pi/N );
a = 2* Ri * tan( radians( 180/N ) ); o
a = 2*Ri*tan( pi/N );
|
Con la lunghezza del lato di base del poligono: a.
Il raggio del circumcerchio:
R = 1/2 * a/sin( radians( 180/N ) ) ); o
R = 1/2 * a/sin( pi/N );
Il raggio del incerchio:
Ri = 1/2 * a/tan( radians( 180/N ) ) ); o
Ri = 1/2 * a/tan( pi/N );
|
|
Polygono regulare - angoli, lati, raggi.
|
|