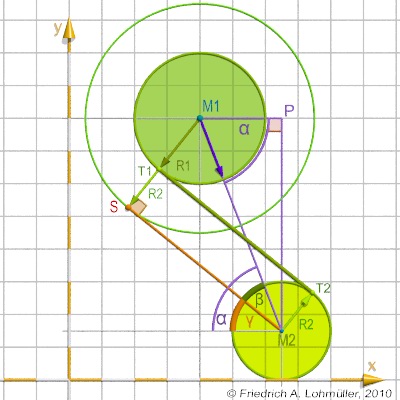
Cerchiamo una tangente interna di due cerchi
di T1 a T2, come nella immagine a margine.
Cerchio 1: M1 = <x1,y1,0>, r1.
Cerchio 2: M2 = <x2,y2,0>, r2. |
Una tangente interna è parallela a un'altra tangente dal centro di un cerchio più picolo (qui: M2)
a un altro cerchio intorno al centro del cerchio più grande (M1) ma con il raggio r1+r2.
--------------------
Per calculo del punto S dobbiamo calculare i lati del triangolo (M2,M1,S).
d(M1,S) = r1+r2 .
Secondo il teorema di Pitagora possiamo calculare:
d(M1,M2) = sqrt((x2-x1)2+(y2-y2)2) .
Cosi il terzi lato (di nuovo con il teorema di Pitagora):
d(M2,S) = sqrt( d(M1,S)2+d(M1,M1)2)
L'angolo entro la direzione di (M1,M2) e la direzione dei x possiamo trovare
con funzioni trigonometriche.
Se x1 < x2 abbiamo
α = abs(degrees( atan ((y2-y1)/(x2-x1))).
altrimenti:
α = 180° - abs(degrees( atan ((y2-y1)/(x2-x1))),
Poi possiamo calulare β e γ come segue:
β = abs( degrees( asin( d(M1, S ) / d(M1,M2) ) )) .
γ = α - β .
La posizione di T1:
xT1 = x1 - r1·cos( Angle(M1S) ).
yT1 = y1 - r1· sin( Angle(M1S) ).
La posizione di T2:
xT2 = x2 + r1·cos( Angle(M1S) ).
yT2 = y2 + r1· sin( Angle(M1S) ).
|
|
Una tangente interna di due cerchi con POV-Ray
Nota: Per evitare collisioni con denominazioni installate e parole riservate
di POV-Ray, si è racommandato assolutamente di usare solo parole con una
maiuscola come lettera iniziale,
per tutte denominazioni di variabili e oggetti dichiarrate degli utenti,
per es. si usa "R1" invece di "r1"
e si usa "Y2" invece di yM2.
#local X1= 0.40; #local Y1= 0.80; #local R1= 0.20;
#local X2= 0.64; #local Y2= 0.15; #local R2= 0.15;
#local M1 = <X1,Y1,0>; #local M2 = <X2,Y2,0>
//------------------------------------------------
#local M_Dist = sqrt(pow(X2-X1,2)+pow(Y2-Y1,2));
#if ( X1 < X2) #local Alpha =
abs( degrees( atan((Y2-Y1)/(X2-X1))));
#else #local Alpha =
180-abs(degrees(atan((Y2-Y1)/(X2-X1))));
#end
#local Beta = abs(degrees(asin((R1+R2)/M_Dist)));
#local Gamma = Alpha - Beta;
#local T1 = M1-<(R1)*cos( radians(Gamma)),
(R1)*sin( radians(Gamma)),0>;
#local T2 = M2+<(R2)*cos( radians(Gamma)),
(R2)*sin( radians(Gamma)),0>; |
Il calcolo della tangente di T1 a T2 in POV-Ray
|