Page d'Accueil
- POV-Ray Tutorial
- Géométrie de Base
pour Raytracing
Triangle rectangle
Théorème de Pythagore
Trigonométrie de base
Loi des cosinus
Triangle équilatéral
Polygone régulier
Polyèdre
Tétraèdre régulier
Octaèdre régulier
Cube et Cuboïde
Dodécaèdre régulier
Icosaèdre régulier
Cuboctaèdre
Octaèdre tronqué
Rhombicuboctaèdre
Icosaèdre tronqué
Cercles
Cercles touchants
Tangentes internes
Tangentes externes
- Geometric 3D Animations
|
Le loi des cosinus
( théorème d'Al-Kashi, théorème de Carnot, théorème de Pythagore généralisé )
Quelques qualités di base sur les côtés et les angles des triangles. |
Note : Les fonctions trigonométriques sin(X), cos(X) et tan(X) en POV-Ray
ont besoin de leurs arguments X en radians !!! Le symbole π = pi en POV-Ray.
Les foctions inverse asin(x), acos(x) et atan(x) donne les angles en radians.
|
Pour chaque triangle ABC
nous avons :
c2 = a2 + b2 - 2*a*b*cos( γ ) (1)
b2 = a2 + c2 - 2*a*c*cos( β ) (2)
a2 = b2 + c2 - 2*b*c*cos( α ) (3)
Pour γ = 90° = pi/2 ( triangle rectangle )
nous avons cos(γ) = 0 e pour cela par (1) :
c2 = a2 + b2 ( Théorème de Pythagore ).
-----------------------------------------------------
Pour les angles de un tiangle ABC
nous avons le formules suivantes :
γ = acos ( ( a2 + b2 - c2 )/(2*a*b) ) (4)
β = acos ( ( a2 + c2 - b2 )/ (2*a*c) ) (5)
α = acos ( ( b2 + c2 - a2 )/ (2*b*c) ) (6)
|
|
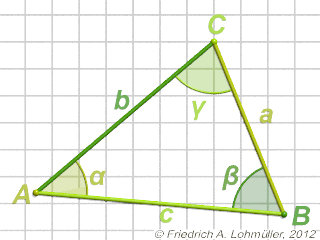
Un triangle ABC en 2D.
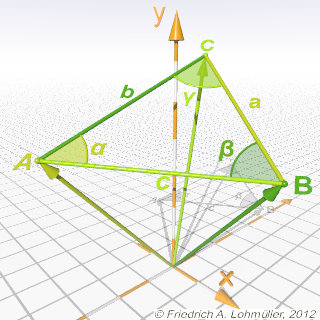
Un triangle ABC en 3D.
|
|