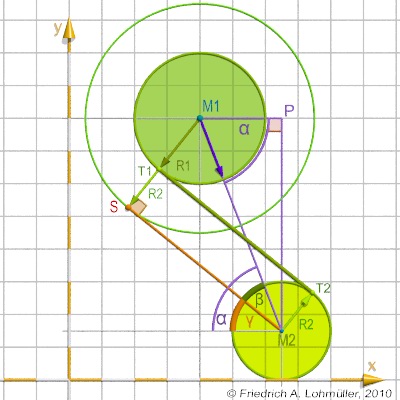
Nous cherchons les tangentes internes aux deux cercles
de T1 à T2, comme figuré sur l'image ci-contre.
Cercle 1: M1 = <x1,y1,0>, r1.
Cercle 2: M2 = <x2,y2,0>, r2. |
Une tangente interne est parallèle à la tangente du centre
du cercle plus petit (Ici: M2)
à un autre cercle autour du centre du cercle plus grand (M1) mais avec le rayon r1+r2.
--------------------
Pour la calulation du point S nous devons calculer les lungueurs des côtés du triangle (M2,M1,S).
d(M1,S) = r1+r2 .
Avec le théorème de Pythagore nous povons calculer :
d(M1,M2) = sqrt((x2-x1)2+(y2-y2)2) .
Ansi le côté troisième (encore avec le théorème de Pythagore):
d(M2,S) = sqrt( d(M1,S)2+d(M1,M1)2)
L'angle entre la direction de (M1,M2) et la direction des x nous pouvons trouver
avec des fonctions trigonométriques .
Si x1 < x2 nous avons :
α = abs(degrees( atan ((y2-y1)/(x2-x1))).
sinon :
α = 180° - abs(degrees( atan ((y2-y1)/(x2-x1))),
Puis nous pouvons calculer β and γ comme suit :
β = abs( degrees( asin( d(M1, S ) / d(M1,M2) ) )) .
γ = α - β .
La position du point T1:
xT1 = x1 - r1·cos( Angle(M1S) ).
yT1 = y1 - r1· sin( Angle(M1S) ).
La position du point T2:
xT2 = x2 + r1·cos( Angle(M1S) ).
yT2 = y2 + r1· sin( Angle(M1S) ).
|
|
Les tangentes internes aux deux cercles rendu avec POV-Ray
Note: Pour eviter chaque collision avec des noms incorporé et des mots réservés
de POV-Ray,
il est très recommandé de utiliser seulement des mots que commencent
avec des capitals (lettres majuscules)
pour tous les noms des variables declarés par le utilisateur, par ex.
on prend "R1" au lieu de "r1"
et "Y2" au lieu de "yM2".
#local X1= 0.40; #local Y1= 0.80; #local R1= 0.20;
#local X2= 0.64; #local Y2= 0.15; #local R2= 0.15;
#local M1 = <X1,Y1,0>; #local M2 = <X2,Y2,0>
//------------------------------------------------
#local M_Dist = sqrt(pow(X2-X1,2)+pow(Y2-Y1,2));
#if ( X1 < X2) #local Alpha =
abs( degrees( atan((Y2-Y1)/(X2-X1))));
#else #local Alpha =
180-abs(degrees(atan((Y2-Y1)/(X2-X1))));
#end
#local Beta = abs(degrees(asin((R1+R2)/M_Dist)));
#local Gamma = Alpha - Beta;
#local T1 = M1-<(R1)*cos( radians(Gamma)),
(R1)*sin( radians(Gamma)),0>;
#local T2 = M2+<(R2)*cos( radians(Gamma)),
(R2)*sin( radians(Gamma)),0>; |
La calulation de la tangente de T1 à T2 en POV-Ray
|