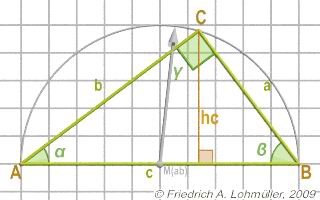
Dimensions et Noms
On appelle hypoténuse c le côté plus long,
c'est le côté opposé à l'angle droit γ à point C.
On appelle cathète chaque côté adjacent à l'angle droit.
Le côté a est opposé à l'angle α
et le e côté b est opposé à l'angle ϐ.
L'angle α est au point A et ϐ est au B. |
α + ϐ = 90 degrees.
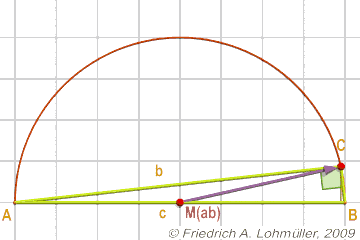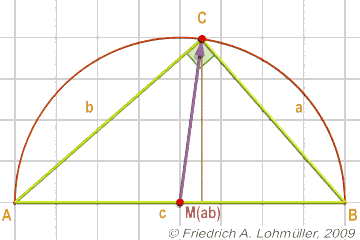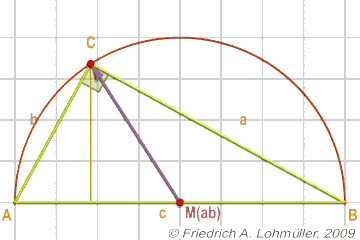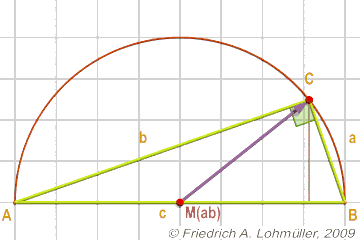
Le rayon du cercle circonscrit au triangle:
R = 1/2 * c = 1/2* d(A,B);
Le théorème de la médiane:
Une règle pour le triangle rectangle:
Si MAB est le centre de l'hypoténuse c, poi CMAB = ½ c.
On peut aussi dire que le point C est situé sur un cercle avec le diamètre [AB].
Pour consequence, si C est un point sur le cercle avec le diamètre [AB],
puis l'angle à C dans le triangle ABC est un angle droit.
|
|
Un triangle rectangle
Un triangle rectangle et le théorème de la médiane,
et le théorème de Thalès - Le cercle de Thalès.
|