Page d'Accueil
- POV-Ray Tutorial
- Géométrie de Base
pour Raytracing
Triangle rectangle
Théorème de Pythagore
Trigonométrie de base
Loi des cosinus
Triangle équilatéral
Polygone régulier
Polyèdre
Tétraèdre régulier
Octaèdre régulier
Cube et Cuboïde
Dodécaèdre régulier
Icosaèdre régulier
Cuboctaèdre
Octaèdre tronqué
Rhombicuboctaèdre
Icosaèdre tronqué
Cercles
Cercles touchants
Tangentes internes
Tangentes externes
- Geometric 3D Animations
|
| |
Polygone régulier
Un polygone régulier est un polygone avec tous les côtés et tous les angles sont égals.
Le triangle équilatéral (3), le carré (4), le pentagone régulier (5), le hexagone régulier (6), le heptagone (7),
le octogone (8), le ennéagone ou nonagone (9), le décagone (10), le hendécagone (11), le dodécagone (12), ... ,
le chiliogone (1000), le myriagone (10000), le megagone (1000000), il gigagone (1000 000 000),
il teragone (1000 000 000 000 000 000), il petagone (1000 000 000 000 000 000 000), ...... le cercle (∞).
|
Note: Les fonctions trigonométriques sin(X), cos(X) et tan(X) en POV-Ray
ont besoin de leurs arguments X en radians !!! Le symbole π = pi en POV-Ray.
|
Le polygone régulier avec N angles ou N cotés :
La somme des angles intérieurs = 180*(N-2);
L'angle extérieur = 180-360/N;
triangle équilatéral: 180-360/3 = 180 - 120 = 60;
carré: 180-360/4 = 180 - 90 = 90;
pentagone régulier: 180-360/5 = 180 - 72 = 108;
hexagone régulier: 180-360/6 = 180 - 60 = 120;
heptagone régulier: 180-360/7 = 180-51,43 = 128,57;
octogone régulier: 180-360/8 = 180 - 45 = 135;
ennéagone régulier: 180-360/8 = 180 - 40 = 140;
décagone régulier: 180-360/8 = 180 - 36 = 144;
hendécagone régulier: 180-360/11= 180 -32,7 = 147,3;
dodécagone régulier: 180-360/12= 180 - 30 = 150; |
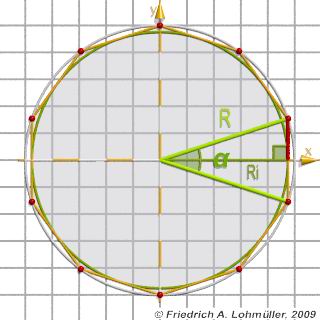
Un polygone régulier avec N angles et
avec le rayon du cercle circonscrit R,
ou avec le rayon du cercle inscrit Ri:
La lunghezza del lato a:
a = 2*R *sin( radians( 180/N ) ); ou
a = 2*R *sin( pi/N );
a = 2*Ri *tan( radians( 180/N ) ); ou
a = 2*Ri*tan( pi/N );
|
Avec la longueur a d'un côté de base du polygone
le rayon du cercle circonscrit:
R = 1/2 * a/sin( radians( 180/N ) ) ); ou
R = 1/2 * a/sin( pi/N );
le rayon du icercle inscrit:
Ri = 1/2 * a/tan( radians( 180/N ) ) ); ou
Ri = 1/2 * a/tan( pi/N );
|
|
Polygone régulier - angles, cotés, rayons.
|
|